题目内容
4.(多选)某人在高层楼房的阳台外侧上以20m/s的速度竖直向上抛出一个石块,石块运动到离抛出点15m处所经历的时间可能是(空气阻力不计,g取10m/s2)( )| A. | 25S | B. | 3S | C. | (2+$\sqrt{7}$)S | D. | (2-$\sqrt{7}$)S |
分析 取竖直向上方向为正方向,竖直上抛运动可以看成一种加速度为-g的匀减速直线运动,当石块运动到抛出点上方离抛出点15m时,位移为x=15m;当石块运动到抛出点下方离抛出点15m时,位移为x=-15m,根据位移公式求出时间.
解答 解:取竖直向上方向为正方向,当石块运动到抛出点上方离抛出点15m时,位移为x=15m,由x=v0t-$\frac{1}{2}$gt2代入得:
15=20t-$\frac{1}{2}$×10t2,解得t1=1s,t2=3s
当石块运动到抛出点下方离抛出点15m时,位移为x=-15m,由x=v0t-$\frac{1}{2}$gt2代入得:
-15=20t-$\frac{1}{2}$×10t2,解得t1=(2+$\sqrt{7}$)s,t2=(2-$\sqrt{7}$)s(舍去).故B、C正确,AD错误.
故选:BC
点评 本题采用整体法研究竖直上抛运动,方法简单,但要注意位移是矢量,与距离不同,不能漏解.

练习册系列答案
相关题目
12.正电子发射计算机断层显象(PET)的基本原理是:将放射性同位素${\;}_{8}^{15}$O注入人体,${\;}_{8}^{15}$O在人体内衰变放出的正电子与人体内的负电子相遇而湮灭转化为一对γ光子,被探测器探测到,经计算机处理后产生清晰的图象.根据PET的原理,下列选项正确的是( )
| A. | ${\;}_{8}^{15}$O的衰变的方程式是:${\;}_{8}^{15}$O→${\;}_{7}^{15}$N+${\;}_{1}^{0}$e | |
| B. | 正负电子湮灭方程式是:${\;}_{1}^{0}$e+${\;}_{-1}^{0}$e→2γ | |
| C. | 在PET中,${\;}_{8}^{15}$O的半衰期随压强的增大而变短. | |
| D. | 在PET中,${\;}_{8}^{15}$O的主要用途是作为示踪原子 | |
| E. | 在PET中,${\;}_{8}^{15}$O的主要用途是参与人体的代谢过程 |
9.某导体中的电流随其两端电压的变化如图所示,则下列说法中正确的是( )


| A. | 加11 V电压时,导体的电阻约是1.4Ω | |
| B. | 加5 V电压时,导体的电阻约是5Ω | |
| C. | 由图可知,随着电压的减小导体的电阻不断减小 | |
| D. | 由图可知,随着电压的增大导体的电阻不断减小 |
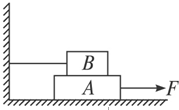 如图所示,物体A重20N,物体B重10N,物体A与物体B、物体A与地面的动摩擦因数相同,用细绳系住物体B,对物体A施加20N的水平向右的拉力时,能将物体A匀速拉出,求接触面间的动摩擦因数.
如图所示,物体A重20N,物体B重10N,物体A与物体B、物体A与地面的动摩擦因数相同,用细绳系住物体B,对物体A施加20N的水平向右的拉力时,能将物体A匀速拉出,求接触面间的动摩擦因数.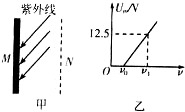 将图甲中所示的装置放在真空中,金属板M受到某种频率为v的紫外线照射时,会不停地发射速度大小及方向都不相同的电子,电子打到金属网N上,在M、N间形成电压,一段时间后,电压达到最大值Um,改变v,Um随之改变,Um-v图线如图乙所示.
将图甲中所示的装置放在真空中,金属板M受到某种频率为v的紫外线照射时,会不停地发射速度大小及方向都不相同的电子,电子打到金属网N上,在M、N间形成电压,一段时间后,电压达到最大值Um,改变v,Um随之改变,Um-v图线如图乙所示.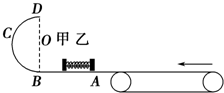 如图所示,右边传送带长L=15m、逆时针转动速度为v0=16m/s,左边是光滑竖直半圆轨道(半径R=0.8m),中间是光滑的水平面AB(足够长).用轻质细线连接甲、乙两物体,中间夹一轻质弹簧,弹簧与甲、乙两物体不拴连.甲的质量为m1=3kg,乙的质量为m2=1kg,甲、乙均静止在光滑的水平面上.现固定甲物体,烧断细线,乙物体离开弹簧后在传送带上滑行的最远距离为sm=12m.传送带与乙物体间动摩擦因数为0.6,重力加速度g取10m/s2,甲、乙两物体可看作质点.
如图所示,右边传送带长L=15m、逆时针转动速度为v0=16m/s,左边是光滑竖直半圆轨道(半径R=0.8m),中间是光滑的水平面AB(足够长).用轻质细线连接甲、乙两物体,中间夹一轻质弹簧,弹簧与甲、乙两物体不拴连.甲的质量为m1=3kg,乙的质量为m2=1kg,甲、乙均静止在光滑的水平面上.现固定甲物体,烧断细线,乙物体离开弹簧后在传送带上滑行的最远距离为sm=12m.传送带与乙物体间动摩擦因数为0.6,重力加速度g取10m/s2,甲、乙两物体可看作质点.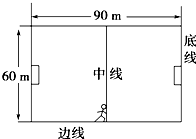 足球比赛中,经常使用“边路突破,下底传中”的战术,即攻方队员带球沿边线前进,到底线附近进行传中,某足球场长90m、宽60m,如图所示.攻方前锋在中线处将足球沿边线向前踢出,足球的运动可视为在地面上做初速度为12m/s的匀减速直线运动,加速度大小为2m/s2.试求:
足球比赛中,经常使用“边路突破,下底传中”的战术,即攻方队员带球沿边线前进,到底线附近进行传中,某足球场长90m、宽60m,如图所示.攻方前锋在中线处将足球沿边线向前踢出,足球的运动可视为在地面上做初速度为12m/s的匀减速直线运动,加速度大小为2m/s2.试求: