Question

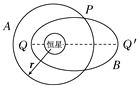
【题目】如图所示，一质量m=1kg的小物块(可视为质点)从A点以大小v0=4m/s的初速度沿切线进入固定光滑圆弧轨道AB，经圆弧轨道后滑上与B点等高、静止在光滑水平面的长木板上，圆弧轨道B端切线水平。已知长木板的质量M=1kg， AO与BO之间夹角θ=37O，BO高5m，小物块与长木板之间的动摩擦因数μ1=0.5。（ sin37O=0.6，cos37O=0.8。）求：

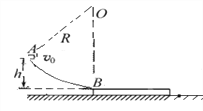
（1）小物块运动至B点时的速度v1大小；

（2）长木板至少为多长，才能保证小物块不滑出长木板？

Answer 1

【答案】（1）（2）1.8m

【解析】（1）小物块沿圆弧轨道从A点到B点应用动能定理：

由几何关系可以得到：

代入数据整理可以得到：

(2)当两物体速度相等时为临界条件

对m根据牛顿第二定律：

对M根据牛顿第二定律：

设t时间两者速度相等，则有：

代入数据可以得到：

木块的位移为：

木板的位移为：

则木板至少需要的长度：

代入数据可以得到：