题目内容
4. 如图所示,将一质量为m的小球从倾角θ=30°的斜面顶点O以一定的初速度水平向右抛出,恰好落在斜面上的A点,求小球的初动能与到达A点时的动能之比.
如图所示,将一质量为m的小球从倾角θ=30°的斜面顶点O以一定的初速度水平向右抛出,恰好落在斜面上的A点,求小球的初动能与到达A点时的动能之比.
分析 根据平抛运动竖直位移和水平位移的关系求出水平分速度和竖直分速度的关系,结合平行四边形定则求出球的初动能与到达A点时的动能之比.
解答 解:根据$tanθ=\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}=\frac{gt}{2{v}_{0}}=\frac{{v}_{y}}{2{v}_{0}}$得,
vy=2v0tanθ=$\frac{2\sqrt{3}}{3}{v}_{0}$.
则小球的初动能与到达A点时的动能之比$\frac{{E}_{k0}}{{E}_{k}}=\frac{\frac{1}{2}m{{v}_{0}}^{2}}{\frac{1}{2}m({{v}_{0}}^{2}+{{v}_{y}}^{2})}$=$\frac{3}{7}$.
答:小球的初动能与到达A点时的动能之比为$\frac{3}{7}$.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,抓住位移关系,结合运动学公式灵活求解.

练习册系列答案
相关题目
14.一质点做简谐运动,先后以相同的速度通过A、B两点,历时1s,质点通过B点后再经过1s又第2次通过B点,在这2s内质点通过的总路程为12cm.则质点的振动周期和振幅分别为( )
| A. | 3s,6cm | B. | 4s,6cm | C. | 4s,9cm | D. | 2s,8cm |
15.关于重心的说法,正确的是( )
| A. | 重心就是物体内最重的一点 | |
| B. | 物体的重心一定在物体上 | |
| C. | 物体的重心可能在物体之外 | |
| D. | 把一物抬到高处,其重心在空间的位置也升高了 |
9.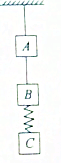 三个质量相同的物块A,B间用一根可伸长的轻橡皮筋相连,B与C用一根轻弹簧相连,A用一根不可伸长的细线挂在天花板上,处于平衡状态,如图所示.已知重力加速度大小为g,现将A与B之间的橡皮筋剪断,在刚剪断橡皮筋的瞬间,三个物体的加速度分别是( )
三个质量相同的物块A,B间用一根可伸长的轻橡皮筋相连,B与C用一根轻弹簧相连,A用一根不可伸长的细线挂在天花板上,处于平衡状态,如图所示.已知重力加速度大小为g,现将A与B之间的橡皮筋剪断,在刚剪断橡皮筋的瞬间,三个物体的加速度分别是( )
 三个质量相同的物块A,B间用一根可伸长的轻橡皮筋相连,B与C用一根轻弹簧相连,A用一根不可伸长的细线挂在天花板上,处于平衡状态,如图所示.已知重力加速度大小为g,现将A与B之间的橡皮筋剪断,在刚剪断橡皮筋的瞬间,三个物体的加速度分别是( )
三个质量相同的物块A,B间用一根可伸长的轻橡皮筋相连,B与C用一根轻弹簧相连,A用一根不可伸长的细线挂在天花板上,处于平衡状态,如图所示.已知重力加速度大小为g,现将A与B之间的橡皮筋剪断,在刚剪断橡皮筋的瞬间,三个物体的加速度分别是( )| A. | 物块A的加速度大小是2g,方向竖直向上 | |
| B. | 物块B的加速度大小是2g,方向竖直向下 | |
| C. | 物块C的加速度大小是g,方向竖直向下 | |
| D. | 物块B的加速度为零 |
16.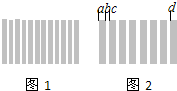 如图所示是两种不同色光用同一个双缝干涉装置做实验得到的干涉图样.(阴影部分表示亮纹,空白处表示暗纹).下列说法中正确的有( )
如图所示是两种不同色光用同一个双缝干涉装置做实验得到的干涉图样.(阴影部分表示亮纹,空白处表示暗纹).下列说法中正确的有( )
 如图所示是两种不同色光用同一个双缝干涉装置做实验得到的干涉图样.(阴影部分表示亮纹,空白处表示暗纹).下列说法中正确的有( )
如图所示是两种不同色光用同一个双缝干涉装置做实验得到的干涉图样.(阴影部分表示亮纹,空白处表示暗纹).下列说法中正确的有( )| A. | 图1对应的色光的频率较低 | |
| B. | 图1对应的色光的波长较大 | |
| C. | 图2中短线bc间的距离就是相邻亮纹间的距离 | |
| D. | 图2中短线ac间的距离就是相邻亮纹间的距离 |
 在一个点电荷Q形成的电场中,建立如图甲所示的Ox坐标轴,坐标轴上A、B两点的坐标分别为2.0m和5.0m.放在A、B两点的试探电荷所受电场力大小跟其电量的关系图象分别如图乙中直线a、b所示.如果放在A点的试探电荷带正电、放在B点的试探电荷带负电,则它们受到的电场力方向都跟x轴的正方向相同.求:
在一个点电荷Q形成的电场中,建立如图甲所示的Ox坐标轴,坐标轴上A、B两点的坐标分别为2.0m和5.0m.放在A、B两点的试探电荷所受电场力大小跟其电量的关系图象分别如图乙中直线a、b所示.如果放在A点的试探电荷带正电、放在B点的试探电荷带负电,则它们受到的电场力方向都跟x轴的正方向相同.求: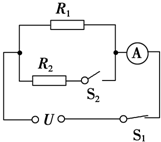 如图9所示的电路中,R1=40Ω,R2=60Ω,电源的电压恒定不变,当开关S2断开时,电流表的示数为0.3A.若将开关S2闭合,求电路中的总电阻和电流表的示数各是多少?
如图9所示的电路中,R1=40Ω,R2=60Ω,电源的电压恒定不变,当开关S2断开时,电流表的示数为0.3A.若将开关S2闭合,求电路中的总电阻和电流表的示数各是多少?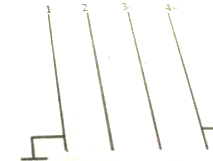 四块金属方块如图放置,边长L、间距d(L>>d)板1带q1(q1<0)的净电荷,板2:2q1,板3:3q1,板4:4q1.现将板1和4接地.
四块金属方块如图放置,边长L、间距d(L>>d)板1带q1(q1<0)的净电荷,板2:2q1,板3:3q1,板4:4q1.现将板1和4接地.