题目内容
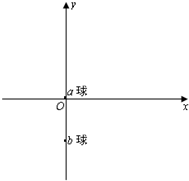 (2010?镇江一模)在光滑绝缘的水平面(纸面)上建有如图所示的平面直角坐标系,在此水平面上可视为质点的不带电小球a静止于坐标系的原点O,可视为质点的带正电小球b静止在坐标为(0,-h)的位置上.现加一方向沿y轴正方向、电场强度大小为E、范围足够大的匀强电场,同时给a球以某一速度使其沿x轴正方向运动.当b球到达坐标系原点O时速度为v0,此时立即撤去电场而改加一方向垂直于纸面向外、磁感应强度大小为B、范围足够大的匀强磁场,最终b球能与a球相遇.求:
(2010?镇江一模)在光滑绝缘的水平面(纸面)上建有如图所示的平面直角坐标系,在此水平面上可视为质点的不带电小球a静止于坐标系的原点O,可视为质点的带正电小球b静止在坐标为(0,-h)的位置上.现加一方向沿y轴正方向、电场强度大小为E、范围足够大的匀强电场,同时给a球以某一速度使其沿x轴正方向运动.当b球到达坐标系原点O时速度为v0,此时立即撤去电场而改加一方向垂直于纸面向外、磁感应强度大小为B、范围足够大的匀强磁场,最终b球能与a球相遇.求:(1)b球的比荷
| q | m |
(2)从b球到达原点O开始至b球与a球相遇所需的时间;
(3)撤去电场时,a球的位置坐标.
分析:(1)b球在电场力作用下做匀加速运动,电场力做功等于b球的动能变化,根据动能定理可求得b球的比荷
;
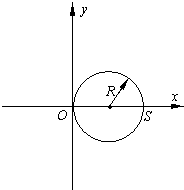
(2)b球到达原点O后在洛伦兹力作用下而做匀速圆周运动,根据牛顿第二定律可求出圆周运动的半径,由圆周运动知识求出周期T.如图,b球只能与a球在图中的S处相遇,即可根据周期性求出时间.
(3)a球从O点开始运动到S点的过程中,b球先做匀加速直线运动,后做匀速圆周运动,a球做匀速直线运动,两球运动的时间相同,即可得到a球从开始运动到两球相遇所用的时间,位移等于b球圆周运动的直径,由公式v=
可求出a球的速度,再由位移公式求解出撤去电场时,a球的位置坐标.
| q |
| m |
(2)b球到达原点O后在洛伦兹力作用下而做匀速圆周运动,根据牛顿第二定律可求出圆周运动的半径,由圆周运动知识求出周期T.如图,b球只能与a球在图中的S处相遇,即可根据周期性求出时间.
(3)a球从O点开始运动到S点的过程中,b球先做匀加速直线运动,后做匀速圆周运动,a球做匀速直线运动,两球运动的时间相同,即可得到a球从开始运动到两球相遇所用的时间,位移等于b球圆周运动的直径,由公式v=
| x |
| t |
解答:解:(1)b球在电场力作用下加速,由动能定理得:qEh=
m
则b球的比荷为
=
(2)b球运动到原点后,只在磁场力作用下,在水平面上做匀速圆周运动,有:qv0B=m
得:R=
b球圆周运动的周期为 T=
=
=
b球只能与a球相遇在图中的S处,相遇所需时间为:
t=(k+
)T=(k+
)
,(k=1,2,3,…)
(3)a球从O点开始运动到S点,与b球相遇所用时间为:t′=t1+t
由h=
t1得:t1=
a球通过的位移为:OS=2R
由v=
可得a球的速度为:v=
则撤去电场时,a球在x轴上的坐标为:x0=vt1=
球的位置为(
,0)(k=1,2,3,…)
答:(1)b球的比荷
为
;
(2)从b球到达原点O开始至b球与a球相遇所需的时间是
,(k=1,2,3,…);
(3)撤去电场时,a球的位置坐标是(
,0)(k=1,2,3,…).
| 1 |
| 2 |
| v | 2 0 |

则b球的比荷为
| q |
| m |
| ||
| 2Eh |
(2)b球运动到原点后,只在磁场力作用下,在水平面上做匀速圆周运动,有:qv0B=m
| ||
| R |
得:R=
| mv0 |
| qB |
b球圆周运动的周期为 T=
| 2πR |
| v0 |
| 2πm |
| qB |
| 4πhE | ||
B
|
b球只能与a球相遇在图中的S处,相遇所需时间为:
t=(k+
| 1 |
| 2 |
| 1 |
| 2 |
| 4πhE | ||
B
|
(3)a球从O点开始运动到S点,与b球相遇所用时间为:t′=t1+t
由h=
| v0 |
| 2 |
| 2h |
| v0 |
a球通过的位移为:OS=2R
由v=
| 2R |
| t1+t |
可得a球的速度为:v=
| 2Ev0 |
| Bv0+(2k+1)πE |
则撤去电场时,a球在x轴上的坐标为:x0=vt1=
| 4Eh |
| Bv0+(2k+1)πE |
球的位置为(
| 4Eh |
| Bv0+(2k+1)πE |
答:(1)b球的比荷
| q |
| m |
| ||
| 2Eh |
(2)从b球到达原点O开始至b球与a球相遇所需的时间是
| 4πhE | ||
B
|
(3)撤去电场时,a球的位置坐标是(
| 4Eh |
| Bv0+(2k+1)πE |
点评:本题的解题关键是分析两球的运动过程,抓住两球运动的同时性,以及b球圆周运动的周期性即可求出时间.

练习册系列答案
相关题目
 (2010?镇江一模)如图所示,长方体物块C置于水平地面上,物块A、B用不可伸长的轻质细绳通过滑轮连接(不计滑轮与绳之间的摩擦),A物块与C物块光滑接触,整个系统中的A、B、C三物块在水平恒定推力F作用下从静止开始以相同的加速度一起向左运动.下列说法正确的是( )
(2010?镇江一模)如图所示,长方体物块C置于水平地面上,物块A、B用不可伸长的轻质细绳通过滑轮连接(不计滑轮与绳之间的摩擦),A物块与C物块光滑接触,整个系统中的A、B、C三物块在水平恒定推力F作用下从静止开始以相同的加速度一起向左运动.下列说法正确的是( )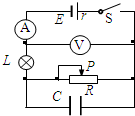 (2010?镇江一模)如图所示的电路,闭合开关S,当滑动变阻器滑片P向右移动时,下列说法正确的是( )
(2010?镇江一模)如图所示的电路,闭合开关S,当滑动变阻器滑片P向右移动时,下列说法正确的是( )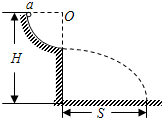 (2010?镇江一模)如图所示,有一光滑的半径可变的
(2010?镇江一模)如图所示,有一光滑的半径可变的