题目内容
13. 如图所示,一根长L=1m的光滑轻质细杆AB与水平面夹角θ=53°,杆上套一质量m=1kg的小球(可看做质点),杆绕过A点的竖直线以某角速度匀速转动时,此时小球刚好位于杆正中间且相对杆静止,g取10m/s2,求:
如图所示,一根长L=1m的光滑轻质细杆AB与水平面夹角θ=53°,杆上套一质量m=1kg的小球(可看做质点),杆绕过A点的竖直线以某角速度匀速转动时,此时小球刚好位于杆正中间且相对杆静止,g取10m/s2,求:(1)杆对球作用力大小及小球转动的角速度?
(2)改变杆的转速,小球将沿杆向上移动,当杆的角速度达到多大时,小球将脱离杆?在此过程中杆对小球做了多少功?
(3)小球脱离杆后落在水平面上,其落点到A点的距离多大?
分析 (1)对小球进行受力分析,结合牛顿第二定律即可求出小球刚好位于杆正中间且相对杆静止时杆的作用力和角速度;
(2)对小球进行受力分析,结合牛顿第二定律即可求出小球上升到杆的最上端时的线速度,然后结合功能关系即可求出杆做的功;
(3)小球脱离杆后做平抛运动,由平抛运动的方法,结合几何关系即可求出.
解答  解:(1)小球刚好位于杆正中间且相对杆静止时受力如图1,则:
解:(1)小球刚好位于杆正中间且相对杆静止时受力如图1,则:
FN•cosθ=mg
所以:${F}_{N}=\frac{mg}{cosθ}=\frac{1×10}{sin53°}=\frac{50}{3}$N
重力与杆的作用力的合力提供向心力,所以:$mr{ω}^{2}={F}_{N}•sinθ=\frac{50}{3}×\frac{4}{5}$=$\frac{40}{3}$N
又:$r=\frac{L}{2}•cos53°$
代入数据得:ω=$\frac{2\sqrt{5gL}}{3}$rad/s
(2)当小球在最高点做圆周运动时,仍然是重力与杆的作用力的合力提供向心力,可知向心力仍然是:$\frac{40}{3}$N
小球做圆周运动的半径:r′=L•cos53°=0.6m
则:$\frac{40}{3}=mω{′}^{2}r′$
代入数据得:ω′=$\frac{10\sqrt{2}}{3}$rad/s
由动能定理得:$-mg•\frac{L}{2}sinθ+W=\frac{1}{2}m(r′ω′)^{2}-\frac{1}{2}m{r}^{2}{ω}^{2}$
代入数据得:W=6J
(3)小球在最高点的速度:${v}_{B}=ω′r′=\frac{10\sqrt{2}}{3}×0.6=2\sqrt{2}$m/s
小球离开B点后做平抛运动,落地的时间:$t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2Lsinθ}{g}}=\sqrt{\frac{2×1×sin53°}{10}}=0.4$s 水平方向的位移:x=${v}_{B}t=2\sqrt{2}×0.4=0.8\sqrt{2}$m
水平方向的位移:x=${v}_{B}t=2\sqrt{2}×0.4=0.8\sqrt{2}$m
如图2画出落地点P与A点、B点在地面上的投影点B′点的几何关系,则:
${r}_{A}=\sqrt{{x}^{2}+(Lcosθ)^{2}}$
代入数据得:${r}_{A}=\frac{\sqrt{41}}{5}$m
答:(1)杆对球作用力大小是$\frac{50}{3}$N,小球转动的角速度是$\frac{2\sqrt{5gL}}{3}$rad/s;
(2)改变杆的转速,小球将沿杆向上移动,当杆的角速度达到$\frac{10\sqrt{2}}{3}$rad/s时,小球将脱离杆;在此过程中杆对小球做功6J;
(3)小球脱离杆后落在水平面上,其落点到A点的距离是$\frac{\sqrt{41}}{5}$m.
点评 本题考查了牛顿第二定律、功能关系、平抛运动与圆周运动的综合,要明确小球做匀速转动时,靠合力提供向心力,由静止释放时,加速度为零时速度最大.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
| A. | 线框中产生感应电动势,可跟随磁铁转动 | |
| B. | 线框中不产生感应电动势,可跟随磁铁转动 | |
| C. | 线框中产生感应电动势,不跟随磁铁转动 | |
| D. | 线框中不产生感应电动势,不跟随磁铁转动 |
| A. | 曲线运动一定是变速运动 | |
| B. | 做平抛运动的某一物体某时水平速度为3m/s,竖直速度4m/s,此时合速度为5m/s | |
| C. | 做平抛运动的某一物体某时水平方向动能3J,竖直方向动能4J,此时物体动能5J | |
| D. | 小船渡河要想时间最短,船头要垂直河岸即可,与水速无关 |
| A. | 不同物体做自由落体运动,它们的运动规律是不同的 | |
| B. | 自由落体运动的加速度与物体的质量大小无关,在任何地方都一样大 | |
| C. | 物体在空气中从静止开始下落的运动一定都是自由落体运动 | |
| D. | 自由落体运动是初速度为0、加速度为g的竖直向下的匀加速直线运动 |
| A. | 推力总小于木箱受到的重力 | |
| B. | 推力总小于木箱受到的支持力 | |
| C. | 推力总小于木箱受到的摩擦力 | |
| D. | 推力小于或等于木箱受到的最大静摩擦力 |
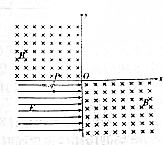 如图所示,在水平面内建立xOy坐标系,在第二、四象限存在磁感应强度相同的匀强磁场,在第三象限设有水平向右的匀强电场.电场强度为E,某带电粒子自x轴上的P点以平行与y轴的速度v0射入电场,已知粒子质量为m,电荷量为q,粒子第一次经过y轴的坐标为(0,$\frac{m{v}_{0}^{2}}{qE}$),不计粒子重力.
如图所示,在水平面内建立xOy坐标系,在第二、四象限存在磁感应强度相同的匀强磁场,在第三象限设有水平向右的匀强电场.电场强度为E,某带电粒子自x轴上的P点以平行与y轴的速度v0射入电场,已知粒子质量为m,电荷量为q,粒子第一次经过y轴的坐标为(0,$\frac{m{v}_{0}^{2}}{qE}$),不计粒子重力. 如图,质量为m的木块放在质量为M的小车上,地面光滑,木块和小车之间动摩擦因数是μ,用水平外力F拉动小车和木块一起作无相对滑动的加速运动.求拉力F的最大值是多少?
如图,质量为m的木块放在质量为M的小车上,地面光滑,木块和小车之间动摩擦因数是μ,用水平外力F拉动小车和木块一起作无相对滑动的加速运动.求拉力F的最大值是多少? 如图所示,在光滑水平轨道上有一质量为M=40kg的小车,另有一质量为m=60kg的人与小车一起以v0=4m/s的速度向左匀速运动,当该人相对小车以μ=2m/s的速度向后跳出时,问:小车速度变为多大?
如图所示,在光滑水平轨道上有一质量为M=40kg的小车,另有一质量为m=60kg的人与小车一起以v0=4m/s的速度向左匀速运动,当该人相对小车以μ=2m/s的速度向后跳出时,问:小车速度变为多大? ,质量m=
,质量m= 的带电正粒子,沿电场中心线RO垂直电场线飞入电场,初速度
的带电正粒子,沿电场中心线RO垂直电场线飞入电场,初速度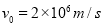 ,粒子飞出平行板电场后经过界面MN、PS间的无电场区域后,进入固定在O点的点电荷Q形成的电场区域,(设界面PS右边点电荷的电场分布不受界面的影响).已知两界面MN、PS相距为12cm,D是中心线RO与界面PS的交点,O点在中心线上,距离界面PS为9cm,粒子穿过界面PS最后垂直打在放置于中心线上的荧光屏bc上,不计粒子重力(静电力常量
,粒子飞出平行板电场后经过界面MN、PS间的无电场区域后,进入固定在O点的点电荷Q形成的电场区域,(设界面PS右边点电荷的电场分布不受界面的影响).已知两界面MN、PS相距为12cm,D是中心线RO与界面PS的交点,O点在中心线上,距离界面PS为9cm,粒子穿过界面PS最后垂直打在放置于中心线上的荧光屏bc上,不计粒子重力(静电力常量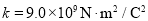 )
)