题目内容
8.某一星球上,宇航员站在距离地面h高度处,以初速度v0沿水平方向抛出一个小球,经时间t后小球落到星球表面,已知该星球的半径为R,引力常量为G,求:(1)该星球表面的重力加速度g;
(2)该星球的第一宇宙速度;
(3)该星球的质量M.
分析 (1)根据平抛运动竖直方向上的运动规律,结合位移时间公式求出星球表面的重力加速度.
(2)根据万有引力提供向心力即可求出该星球的第一宇宙速度.
(3)根据万有引力等于重力求出星球的质量.
解答 解:(1)平抛运动的物体在竖直方向做自由落体运动,根据h=$\frac{1}{2}g{t}^{2}$得星球表面的重力加速度为:g=$\frac{2h}{{t}^{2}}$.
(2)星球表面的重力提供卫星绕其表面做匀速圆周运动的向心力,则有:mg=$\frac{m{v}^{2}}{R}$
所以有:v=$\sqrt{gR}$=$\frac{1}{t}•\sqrt{2hR}$
(3)根据$G\frac{Mm}{{R}^{2}}=mg$得星球的质量为:M=$\frac{g{R}^{2}}{G}=\frac{2h{R}^{2}}{G{t}^{2}}$.
答:(1)该星球表面的重力加速度g是$\frac{2h}{{t}^{2}}$;
(2)该星球的第一宇宙速度是$\frac{1}{t}•\sqrt{2hR}$;
(3)该星球的质量M是$\frac{2h{R}^{2}}{G{t}^{2}}$.
点评 该题考查万有引力定律的应用,解决本题的关键掌握万有引力等于重力这一理论,并能灵活运用.

练习册系列答案
相关题目
18.某中学正在举行班级对抗赛,张明明同学是短跑运动员,在100米竞赛中,测得他在前50m的平均速度为10.4m/s,在后50m的平均速度为10.2m/s,该同学10s末到达终点,则他在全程中的平均速度为( )
| A. | 10m/s | B. | 10.3 m/s | C. | 10.2 m/s | D. | 10.4 m/s |
16.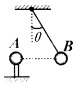 如图所示,一个挂在丝线下端的 带正电的小球B静止在图示位置.固定的带正电荷的A球电荷量为Q,B球质量为m、电荷量为q,θ=30°,A和B在同一水平线上,整个装置处在真空中,求A、B两球间的距离.
如图所示,一个挂在丝线下端的 带正电的小球B静止在图示位置.固定的带正电荷的A球电荷量为Q,B球质量为m、电荷量为q,θ=30°,A和B在同一水平线上,整个装置处在真空中,求A、B两球间的距离.
 如图所示,一个挂在丝线下端的 带正电的小球B静止在图示位置.固定的带正电荷的A球电荷量为Q,B球质量为m、电荷量为q,θ=30°,A和B在同一水平线上,整个装置处在真空中,求A、B两球间的距离.
如图所示,一个挂在丝线下端的 带正电的小球B静止在图示位置.固定的带正电荷的A球电荷量为Q,B球质量为m、电荷量为q,θ=30°,A和B在同一水平线上,整个装置处在真空中,求A、B两球间的距离.
3.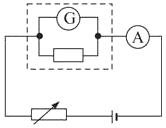 如图所示,将一个改装的电流表接入电路进行校准,发现待测表的读数比标准表的读数偏大一些,如表头G的I g 是准确的,出现的误差可能是下述哪种原因引起的( )
如图所示,将一个改装的电流表接入电路进行校准,发现待测表的读数比标准表的读数偏大一些,如表头G的I g 是准确的,出现的误差可能是下述哪种原因引起的( )
 如图所示,将一个改装的电流表接入电路进行校准,发现待测表的读数比标准表的读数偏大一些,如表头G的I g 是准确的,出现的误差可能是下述哪种原因引起的( )
如图所示,将一个改装的电流表接入电路进行校准,发现待测表的读数比标准表的读数偏大一些,如表头G的I g 是准确的,出现的误差可能是下述哪种原因引起的( )| A. | Rg 的测量值比真实值偏大 | |
| B. | Rg 的测量值比真实值偏小 | |
| C. | 所并联的R 并′比公式R 并′=$\frac{I_gR_g}{I-I_g}$计算出的R 并′偏小 | |
| D. | 所并联的R 并′比公式R 并′=$\frac{I_gR_g}{I-I_g}$ 计算出的R 并′偏大 |
20. A、B两辆汽车从同一地点在同一直线上做匀变速直线运动,它们的速度-时间图象如图所示,则在6s内( )
A、B两辆汽车从同一地点在同一直线上做匀变速直线运动,它们的速度-时间图象如图所示,则在6s内( )
 A、B两辆汽车从同一地点在同一直线上做匀变速直线运动,它们的速度-时间图象如图所示,则在6s内( )
A、B两辆汽车从同一地点在同一直线上做匀变速直线运动,它们的速度-时间图象如图所示,则在6s内( )| A. | A、B两辆汽车运动方向相反 | B. | A车的加速度小于B车的加速度 | ||
| C. | t=4s时,A、B两辆汽车相距最远 | D. | t=4s时,A、B两辆汽车刚好相遇 |
17.某潜水爱好者练习潜水.某次竖直方向潜水的v-t图象如图所示,下列说法正确的是( )
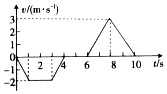

| A. | 本次下潜的最大深度为6m | |
| B. | 全过程中,该潜水爱好者的最大加速度是1.5m/s2 | |
| C. | 0~6s时间内,潜水爱好者平均速度大小为1.5m/s | |
| D. | 0一10s时间内,潜水爱好者的平均速度为零 |
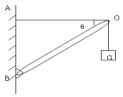 如图所示,一轻质硬杆OB可绕通过B点且垂直于纸面的轴转动,另一端与水平绳OA相连,在O点悬挂一重为G的物体,∠AOB=θ,求轻绳对O点的拉力和轻杆OB对O点的支持力分别为多大?
如图所示,一轻质硬杆OB可绕通过B点且垂直于纸面的轴转动,另一端与水平绳OA相连,在O点悬挂一重为G的物体,∠AOB=θ,求轻绳对O点的拉力和轻杆OB对O点的支持力分别为多大?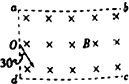 一足够长的矩形区域abcd内充满磁感应强度为B、方向垂直纸面向里的匀强磁场,矩形区域的左边界ad长为L,现从ad中点O垂直于磁场射入一速度方向与ad边夹角为30°、大小为v0的带正电粒子,如图所示,已知粒子电荷量为q,质量为m(重力不计).若要求粒子能从ab边射出磁场,v0应满足什么条件?
一足够长的矩形区域abcd内充满磁感应强度为B、方向垂直纸面向里的匀强磁场,矩形区域的左边界ad长为L,现从ad中点O垂直于磁场射入一速度方向与ad边夹角为30°、大小为v0的带正电粒子,如图所示,已知粒子电荷量为q,质量为m(重力不计).若要求粒子能从ab边射出磁场,v0应满足什么条件?