��Ŀ����
����Ŀ��2019��1��3�š��϶�4�š�̽����ʵ�������״���������½������չѲ��̽�⡣������û�д�������ͨ������ɡ������½������ͨ������������ʵ�ּ��١���ͼ��ʾΪ���϶�4�š�̽�����������������̵ļ�ģ�͡�����m��̽�����ذ뾶Ϊr��Բ���I�����˶���Ϊʹ̽������ȫ��½��������P���ع�����߷�����ǰ���ٶ�u��������Ϊ��m�����壬�Ӷ�ʹ̽������P������Բ���IIת��Q�㣨��Բ�����������Q�����У�ʱǡ�õ���������渽�����ٴ���ǰ���������½����֪��������ΪM���뾶ΪR��������������ΪG��������˵����ȷ���ǣ�������

A.̽������������ǰ��Բ�ܹ��I������ʱ������Ϊ![]()
B.��P��̽��������������ٶȴ�С��Ϊ![]()
C.���ٽ�����̣���P���ع��II���е����������������ʱ��Ϊ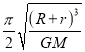
D.��������������ٶȵĴ�СΪ![]()
���𰸡�AD
��������
A��̽����������������Բ���˶������������ṩ������
![]()
���̽������������ǰ��Բ�ܹ��I������ʱ������
![]()
��A��ȷ��
B����P��̽������������Ĺ����У�������ǰ���ٶ�Ϊv�����ݶ����غ��֪
mv=��mu+��m-��m��v'
��������̽�������ٶ�
![]()
��B����
C��̽�����ڹ��II������Բ�˶����볤��
![]()
���ݿ����յ������ɿ�֪
![]()
���
![]()
���ٽ�����̣���P���ع��II���е����������������ʱ��Ϊ
![]()
��C����
D���������������ķ���һ������Ϊm�����壬�����ܵ��������������������
![]()
�����������������ٶȵĴ�С
![]()
��D��ȷ��
��ѡAD��

 ��������������������ϵ�д�
��������������������ϵ�д�