��Ŀ����
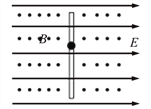
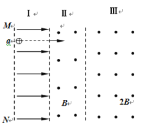
����Ŀ����ͼ��ʾ����ƽ�н��������ľ���L=0.4m�������������ڵ�ƽ����ˮƽ��н���=37�����ڵ�������ƽ���ڣ��ֲ��ŴŸ�Ӧǿ��B=0.5T������ֱ�ڵ�������ƽ��ľֲ���ǿ�ų������������һ�˽��е綯��E=4.5V������r=0.5����ֱ����Դ���ְ�һ������m=0.04kg�ĵ����ab���ڽ��������ϣ������ǡ�þ�ֹ���������������촹ֱ���ҽӴ����ã���������������Ӵ��������ĵ���R0=2.5��������������費�ơ�����֪���Ħ�������ڻ���Ħ�������ֲ���ǿ�ų�ȫ�����ǵ����ab����δ���ǵ�Դ��
��1����ֹʱ������ܵ��İ�����F����С��Ħ����f��С��
��2�������������������Ϊԭ�����������ų����Ժ㶨�ٶ�v1=30m/s�ع�������˶���ǡ��ʹ�õ���������ϻ������ֲ���ǿ�ų������˶�������ʼ�ո��ǵ����ab����δ���ǵ�Դ��������ϻ��ٶ�v2��
��3�������⣨2���е���������ϻ��Ĺ��̣��������Ĺ���P����ȫ��·�еĵ繦��P����
���𰸡���1��0.3N��0.06N����2��7.5m/s����3��4.5W��27W��
��������
��1������������������ֱ����Դ���ɱպϵ�·�����ݱպϵ�·ŷķ���ɣ���
I=![]()
�����ֶ�������ܵİ�����ƽ�е���ƽ�����ϣ����С
F��=BIL=0.30N
���������������б�����µķ���Ϊ��
F1=mgsin37��=0.24N
����F1С�ڰ��������ʵ��������б�����µ�Ħ����f�����ݹ�����ƽ����������
mgsin37��+f=F��
���Ħ����
f=0.06N
��2��������������ӱ���ʹ�������˶���Ҫ�İ�����ҲӦ�üӱ�
F����=0.60N
�赼��������ϻ����ٶ�Ϊv2����·�еĵ綯��
E=BL��v1��v2��+E
I=![]()
F����=BIL
�������ݣ�������ϻ��ٶ�
v2=7.5 m/s
��3������������
P��=F����![]() v2=0.6
v2=0.6![]() 7.5W=4.5W
7.5W=4.5W
E��=BL��v1��v2��+E=9V
ȫ��·�еĵ繦��
P��=![]() =27W
=27W
�𣺣�1����ֹʱ������ܵ��İ�����F����СΪ0.3N��Ħ����f��СΪ0.06N����2��������ϻ��ٶ�Ϊ7.5m/s����3���������Ĺ���P��Ϊ4.5W��ȫ��·�еĵ繦��P��Ϊ27W��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�