题目内容
阅读如下资料并回答问题:
自然界中的物体由于具有一定的温度,会不断向外辐射电磁波,这种辐射因与温度有关,称为热辐射.热辐射具有如下特点:辐射的能量中包含各种波长的电磁波;物体温度越高,单位时间内从物体表面单位面积上辐射的能量越大;在辐射的总能量中,各种波长所占的百分比不同.
处于一定温度的物体在向外辐射电磁波能量的同时,也要吸收由其他物体辐射的电磁能量,如果它处于平衡状态,则能量保持不变.若不考虑物体表面性质对辐射与吸收的影响,我们定义一种理想的物体,它能100%地吸收入射到其表面的电磁辐射,这样的物体称为黑体.单位时间内从黑体表面单位面积辐射的电磁波的总能量与热力学温度的四次方成正比.即P0=δT4,其中常量δ=5.67×10-8 W/(m2·K4).
在下面的问题中,把研究对象都简单地看作黑体,有关数据及数学公式:太阳半径RS="696" 000 km,太阳表面温度T="5" 770 K,火星半径r="3" 395 km,球面面积S=4πR2,其中R为半径.
(1)太阳热辐射能量的绝大多数集中在波长为2×10-7—1×102 m范围,求相应的频率范围.
(2)每小时从太阳表面辐射的总能量是多少?
(3)火星受到来自太阳的辐射可认为垂直射到面积为πr2(r为火星半径)的圆盘上,已知太阳到火星的距离为太阳半径的400倍,忽略其他天体及宇宙空间的辐射,试估算火星的平均温度.
自然界中的物体由于具有一定的温度,会不断向外辐射电磁波,这种辐射因与温度有关,称为热辐射.热辐射具有如下特点:辐射的能量中包含各种波长的电磁波;物体温度越高,单位时间内从物体表面单位面积上辐射的能量越大;在辐射的总能量中,各种波长所占的百分比不同.
处于一定温度的物体在向外辐射电磁波能量的同时,也要吸收由其他物体辐射的电磁能量,如果它处于平衡状态,则能量保持不变.若不考虑物体表面性质对辐射与吸收的影响,我们定义一种理想的物体,它能100%地吸收入射到其表面的电磁辐射,这样的物体称为黑体.单位时间内从黑体表面单位面积辐射的电磁波的总能量与热力学温度的四次方成正比.即P0=δT4,其中常量δ=5.67×10-8 W/(m2·K4).
在下面的问题中,把研究对象都简单地看作黑体,有关数据及数学公式:太阳半径RS="696" 000 km,太阳表面温度T="5" 770 K,火星半径r="3" 395 km,球面面积S=4πR2,其中R为半径.
(1)太阳热辐射能量的绝大多数集中在波长为2×10-7—1×102 m范围,求相应的频率范围.
(2)每小时从太阳表面辐射的总能量是多少?
(3)火星受到来自太阳的辐射可认为垂直射到面积为πr2(r为火星半径)的圆盘上,已知太阳到火星的距离为太阳半径的400倍,忽略其他天体及宇宙空间的辐射,试估算火星的平均温度.
(1)3×1013—1.5×1015 Hz (2)1.38×1030 J(3)204 K
(1)v=c/λ得: v1=(3.00×108)/(2×10-7) Hz=1.5×10 15 Hz,v2=(3.00×108)/(2×10-5) Hz=3×1013 Hz
所以辐射频率范围是3×1013—1.5×1015 Hz.
(2)每小时从太阳表面辐射的总能量为:
E=4πδRS2T4t,代入数据得E=1.38×1030 J.
(3)设火星表面温度为T′,太阳到火星的距离为d,火星单位时间内吸收来的太阳辐射能量为P入=4πδRS2T4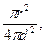 d=400RS,所以P入=πδT4r2/(400)2
d=400RS,所以P入=πδT4r2/(400)2
火星单位时间内向外辐射的电磁波能量为P出=4πδr2T′4,火星处于平衡状态P入=P出,即πδT4r2/(400)2=4πδr2T′4得T′=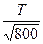 ="204" K.
="204" K.
所以辐射频率范围是3×1013—1.5×1015 Hz.
(2)每小时从太阳表面辐射的总能量为:
E=4πδRS2T4t,代入数据得E=1.38×1030 J.
(3)设火星表面温度为T′,太阳到火星的距离为d,火星单位时间内吸收来的太阳辐射能量为P入=4πδRS2T4
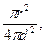 d=400RS,所以P入=πδT4r2/(400)2
d=400RS,所以P入=πδT4r2/(400)2火星单位时间内向外辐射的电磁波能量为P出=4πδr2T′4,火星处于平衡状态P入=P出,即πδT4r2/(400)2=4πδr2T′4得T′=
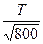 ="204" K.
="204" K.
练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目