题目内容
 如图所示,一个有界的匀强磁场,磁感应强度B=0.50T,磁场方向垂直于纸面向里,MN是磁场的左边界.在距磁场左边界MN的1.0m处有一个放射源A,内装放射物质
如图所示,一个有界的匀强磁场,磁感应强度B=0.50T,磁场方向垂直于纸面向里,MN是磁场的左边界.在距磁场左边界MN的1.0m处有一个放射源A,内装放射物质226 88 |
226 88 |
(1)写出Ra的衰变方程;
(2)求衰变后Rn(氡)的速率(质子、中子的质量为1.6×10-27kg,电子电量e=1.6×10-19C).
分析:(1)根据电荷数守恒、质量数守恒写出衰变方程.
(2)根据带电粒子在匀强磁场中的半径公式以及动量守恒定律求出衰变后Rn(氡)的速率.
(2)根据带电粒子在匀强磁场中的半径公式以及动量守恒定律求出衰变后Rn(氡)的速率.
解答:解:(1)衰变方程为:
Ra→
Rn+
He.
(2)对α粒子,qvB=m
则vα=
.
由动量守恒得,0=mvα-Mv
v=
vα=
=
m/s=4.5×105m/s.
答:(1)衰变方程为:
Ra→
Rn+
He.
(2)衰变后Rn(氡)的速率为4.5×105m/s.
226 88 |
222 86 |
4 2 |
(2)对α粒子,qvB=m
| vα2 |
| r |
则vα=
| qBR |
| m |
由动量守恒得,0=mvα-Mv
v=
| m |
| M |
| qBR |
| M |
| 2×1.6×10-19×1×0.5 |
| 222×1.6×10-27 |
答:(1)衰变方程为:
226 88 |
222 86 |
4 2 |
(2)衰变后Rn(氡)的速率为4.5×105m/s.
点评:解决本题的关键知道在衰变方程中电荷数守恒、质量数守恒,以及知道静止的
Ra发生α衰变,生成的新核动量大小相等,反向相反.
226 88 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
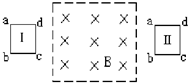 如图所示,一个有界的匀强磁场区域,方向垂直纸面向里,一个矩形闭合导线框abcd沿纸面由位置Ⅰ匀速运动到位置Ⅱ,在导线框进入磁场时,感应电流方向为
如图所示,一个有界的匀强磁场区域,方向垂直纸面向里,一个矩形闭合导线框abcd沿纸面由位置Ⅰ匀速运动到位置Ⅱ,在导线框进入磁场时,感应电流方向为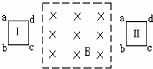 (A)如图所示,一个有界的匀强磁场区域,方向垂直纸面向里,一个矩形闭合导线框abcd沿纸面由位置Ⅰ运动到位置Ⅱ,在dc边刚进入磁场时,受到的安培力方向为
(A)如图所示,一个有界的匀强磁场区域,方向垂直纸面向里,一个矩形闭合导线框abcd沿纸面由位置Ⅰ运动到位置Ⅱ,在dc边刚进入磁场时,受到的安培力方向为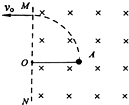 (1)下列说法正确的是
(1)下列说法正确的是