题目内容
(1)已知能使某金属产生光电效应的极限频率为υ0,当用频率为2υ0的单色光照射该金属时,所产生的光电子的最大初动能为
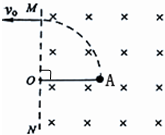 (2)如图所示,一个有界的匀强磁场,磁感应强度B=0.50T,磁场方向垂直于纸面向里,MN是磁场的左边界.在距磁场左边界MN的1.0m处有一个放射源A,内装放射物质
(2)如图所示,一个有界的匀强磁场,磁感应强度B=0.50T,磁场方向垂直于纸面向里,MN是磁场的左边界.在距磁场左边界MN的1.0m处有一个放射源A,内装放射物质
Ra(镭),
Ra发生α衰变生成新核Rn(氡).放在MN左侧的粒子接收器接收到垂直于边界MN方向射出的α粒子,此时接收器位置距直线OA的距离为1.0m.
①试写出Ra的衰变方程;
②求衰变后Rn(氡)的速率.(质子、中子的质量为1.6×10-27kg,电子电量e=1.6×10-19C)
hγ0
hγ0
.当照射光的频率继续增大时,则逸出功不变
不变
(填“增大”“减小”或“不变”) (2)如图所示,一个有界的匀强磁场,磁感应强度B=0.50T,磁场方向垂直于纸面向里,MN是磁场的左边界.在距磁场左边界MN的1.0m处有一个放射源A,内装放射物质
(2)如图所示,一个有界的匀强磁场,磁感应强度B=0.50T,磁场方向垂直于纸面向里,MN是磁场的左边界.在距磁场左边界MN的1.0m处有一个放射源A,内装放射物质226 88 |
226 88 |
①试写出Ra的衰变方程;
②求衰变后Rn(氡)的速率.(质子、中子的质量为1.6×10-27kg,电子电量e=1.6×10-19C)
分析:(1)根据爱因斯坦光电效应方程分析光电子的最大初动能.逸出功由金属材料决定.
(2)①根据质量数守恒和电荷数据守恒,书写Ra的衰变方程.
②衰变后α粒子在磁场中做匀速圆周运动,由洛伦兹力提供向心力,根据牛顿第二定律列式,得到速率的表达式.再根据衰变过程动量守恒,求解衰变后Rn(氡)的速率.
(2)①根据质量数守恒和电荷数据守恒,书写Ra的衰变方程.
②衰变后α粒子在磁场中做匀速圆周运动,由洛伦兹力提供向心力,根据牛顿第二定律列式,得到速率的表达式.再根据衰变过程动量守恒,求解衰变后Rn(氡)的速率.
解答:解:(1)根据爱因斯坦光电效应方程得:Ekm=h?2γ0-W
又W=hγ0
解得,光电子的最大初动能为Ekm=hγ0.
逸出功由金属材料决定,当照射光的频率继续增大时,逸出功不变..
(2)①Ra的衰变方程为
Ra→
Rn+
He;
对α粒子,由qvB=m
,得vα=
对于衰变过程遵守动量守恒,则得0=mvα-Mv
联立上两式得,衰变后Rn(氡)的速率为 v=
=
=
m/s=4.5×105m/s
故答案为:
(1)hv0,不变.
(2)①Ra的衰变方程为
Ra→
Rn+
He;
②衰变后Rn(氡)的速率是4.5×105m/s.
又W=hγ0
解得,光电子的最大初动能为Ekm=hγ0.
逸出功由金属材料决定,当照射光的频率继续增大时,逸出功不变..
(2)①Ra的衰变方程为
226 88 |
222 86 |
4 2 |
对α粒子,由qvB=m
| ||
| r |
| qBr |
| m |
对于衰变过程遵守动量守恒,则得0=mvα-Mv
联立上两式得,衰变后Rn(氡)的速率为 v=
| mvα |
| M |
| qBr |
| M |
| 2×1.6×10-19×1.0×0.5 |
| 222×1.6××10-27 |
故答案为:
(1)hv0,不变.
(2)①Ra的衰变方程为
226 88 |
222 86 |
4 2 |
②衰变后Rn(氡)的速率是4.5×105m/s.
点评:解决本题的关键掌握光电效应的规律,知道在衰变方程中电荷数守恒、质量数守恒,以及知道原子核衰变过程,遵守动量守恒等等规律.

练习册系列答案
相关题目
【物理——选修3—5】(15分)
(1)(5分)下列说法正确的是 。
| A.根据E=mc2可知物体所具有的能量和它的质量之间存在着简单的正比关系 |
B.在单缝衍射实验中,假设只让一个光子通过单缝,则该光 子不可能落在暗条纹处 子不可能落在暗条纹处 |
| C.一群氢原子从n=3的激发态向较低能级跃迁,最多可放出二种频率的光子 |
| D.已知能使某金属发生光电效应的极限频率为ν0,则当频率为2ν0的单色光照射该金属时,光电子的最大初动能为2hν0 |


