题目内容
质量为m的探月航天器在离月球表面高度为R的轨道上飞行,其运动视为匀速圆周运动.已知月球质量为M,月球半径也为R,月球表面重力加速度为g,引力常量为G,不考虑月球自转的影响,则航天器的( )
A、角速度ω=
| ||||
B、线速度v=
| ||||
C、运行周期T=2π
| ||||
D、向心加速度a=
|
分析:根据万有引力提供向心力,结合万有引力等于重力求出角速度、线速度、向心加速度和周期的大小.
解答:解:根据G
=ma=m
=m?2Rω2=m?2R
得,角速度ω=
,线速度v=
,周期T=
,向心加速度a=
.
因为GM=gR2.
解得角速度ω=
,线速度v=
,周期T=4π
,向心加速度a=
.故B正确,A、C、D错误.
故选:B.
| Mm |
| (2R)2 |
| v2 |
| 2R |
| 4π2 |
| T2 |
|
|
|
| GM |
| (2R)2 |
因为GM=gR2.
解得角速度ω=
|
|
|
| g |
| 4 |
故选:B.
点评:解决本题的关键掌握万有引力两个理论的运用:1、万有引力提供向心力;2、万有引力等于重力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
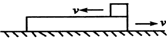 (2012?闵行区三模)(A) 如图,质量为M=3kg的木板放在光滑水平面上,质量为m=1kg的物块在木板上,它们之间有摩擦,木板足够长,两者都以v=4m/s的初速度向相反方向运动,当木板的速度为v1=2.4m/s时,物块的速度是
(2012?闵行区三模)(A) 如图,质量为M=3kg的木板放在光滑水平面上,质量为m=1kg的物块在木板上,它们之间有摩擦,木板足够长,两者都以v=4m/s的初速度向相反方向运动,当木板的速度为v1=2.4m/s时,物块的速度是