题目内容

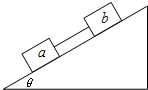
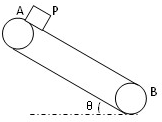
如图所示，倾角θ=37°的传送带上，上、下两端相距S=7m．当传送带以u=4m/s的恒定速率顺时针转动时，将一个与传送带间动摩擦因数μ=0.25的物块P轻放于A端，P从A端运动到B端所需的时间是多少？
设P初始下滑的加速度为a1，则有mgsinθ+μmgcosθ=ma1
解得a1=g(sinθ+μcosθ)=8m/s2
前一段加速滑下时间t1=
u
a
=0.5s
当P加速到u时，P发生的位移S1=
u2
2a1
=1m＜7m
此后P，继续加速下滑，设加速度为a2，
有mgsinθ-μmgcosθ=ma2，所以a2=4m/s2
根据位移时间关系公式，有L-S1=ut2+
1
2
a2
t22

解得后一段加速滑下时间t2=1s
P从A到B总时间t=t1+t2=1.5s
即P从A端运动到B端所需的时间是为1.5s．
练习册系列答案
相关题目
如图所示，长直杆CPD与水平面成45°，由不同材料拼接面成，P为两材料分界点，DP＞CP．一个圆环套在长直杆上，让圆环无初速从顶端滑到底端（如左图）；再将长直杆两端对调放置，让圆环无初速从顶端滑到底端（如右图），两种情况下圆环从开始运动到经过P点的时间相同．下列说法中正确的是（　　）
A．圆环与直杆CP段的动摩擦因数小于圆环与直杆DP段之间的动摩擦因数
B．两次滑动中圆环到达底端速度大小相等
C．两次滑动中圆环到达底端所用时间相等
D．两次滑动到达底端的过程中圆环与直杆摩擦产生的热量相等
一天平放在电梯中，当电梯静止时，在天平左盘上放一物体，右盘上放质量为0.1kg的砝码，天平平衡，当电梯以2m/s2的加速度竖直向上做匀加速直线运动时，g=10m/s2．则（　　）
A．天平仍然平衡
B．物体的质量为0.12g
C．物体对天平左盘的压力大小为1.0N
D．物体对天平左盘的压力大小为1.2N
如图所示，两个木块的质量关系是ma=2mb，用细线连接后放在倾角为θ的光滑固定斜面上．在它们沿斜面自由下滑的过程中，下列说法中正确的是（　　）
A．它们的加速度大小关系是aa＜ab
B．它们的加速度大小相等，且a＜gsinθ
C．连接它们的细线上的张力一定为零
D．连接它们的细线上的张力一定不为零
如图所示，物体m放在升降机中的斜面上，处于静止状态，当升降机开始竖直向上做匀加速直线运动时，（　　）
A．斜面对物体的支持力增大
B．物体m所受的合力增大
C．物体m所受重力增大
D．物体m所受摩擦力增大
一质量为5kg的物体静止放在动摩擦因数为μ=0.2的水平面上，若将一个大小为F=20N的水平拉力作用在该物体上，g取10m/s2．求：
（1）该物体的加速度是多少？
（2）该物体在4s内的位移是多少？
人站在体重计上，当下蹲和起立时，能看到超重和失重的现象，如图所示，小女孩从站立到下蹲过程中，指针示数的变化应是（　　）
A．先增加，后还原B．先减小，后还原
C．先增加，后减小，再还原D．先减小，后增加，再还原
如图所示，航空母舰上的水平起飞跑道长度L=160m．一架质量为m=2.0×104kg的飞机从跑道的始端开始，在大小恒为F=1.2×105N的动力作用下，飞机做匀加速直线运动，在运动过程中飞机受到的平均阻力大小为Ff=2×104N．飞机可视为质点，取g=10m/s2．求：
（1）飞机在水平跑道运动的加速度大小；
（2）若航空母舰静止不动，飞机加速到跑道末端时速度大小；
（3）若航空母舰沿飞机起飞的方向以10m/s匀速运动，飞机从始端启动到跑道末端离开．这段时间内航空母舰对地位移大小．
一质量m=0.5kg的滑块以一定的初速度冲上一倾角为37°足够长的斜面，某同学利用DIS实验系统测出了滑块冲上斜面过程中多个时刻的瞬时速度，如图所示为通过计算机绘制出的滑块上滑过程的v-t图．求：（g取10m/s2）
（1）滑块冲上斜面过程中的加速度大小；
（2）滑块与斜面间的动摩擦因数；
（3）判断滑块最后能否返回斜面底端？若能返回，求出返回斜面底端时的动能；若不能返回，求出滑块停在什么位置．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网