题目内容
【题目】如图所示,一直角三棱镜放置在真空中,其截面三角形的斜边BC的长度为d,一束单色光从AB侧面的中点垂直AB入射.若三棱镜的折射率为 ![]() ,∠C=30°,单色光在真空中的传播速度为c,求:
,∠C=30°,单色光在真空中的传播速度为c,求: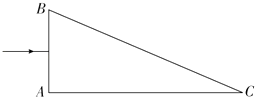
①该单色光第一次从棱镜射入真空时的折射角;
②该单色光从进入棱镜到第一次从棱镜射出所经历的时间.
【答案】解:①画出该单色光在三棱镜中传播的光路图如图所示.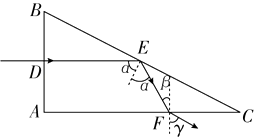
当光线到达三棱镜的BC边时,因∠C=30°,由几何关系可知α=60°
又因为三棱镜的折射率n= ![]() ,所以光发生全反射的临界角为45°
,所以光发生全反射的临界角为45°
因α=60°,所以该单色光在BC边发生全反射.
当该单色光到达三棱镜的AC边时,由几何关系可知,其入射角为β=30°
设其折射角为γ,则由折射定律n= ![]() 可得:γ=45°
可得:γ=45°
②因为截面三角形的斜边BC的长度为d,D为AB边的中点,∠C=30°,由几何关系可知 ![]() =
= ![]()
因为α=60°,所以∠CEF=30°,又∠C=30°,由几何关系可知 ![]() =
= ![]()
该单色光在三棱镜中的传播速度为v= ![]() =
= ![]()
所以单色光从进入棱镜到第一次从棱镜射出所经历的时间t= ![]()
代入数据可解得:t= ![]()
答:①该单色光第一次从棱镜射入真空时的折射角是45°;
②该单色光从进入棱镜到第一次从棱镜射出所经历的时间是 ![]()
【解析】①画出光路图,判断光线在AB面和BC面上能否发生全反射,由几何知识求出光线第一次射入空气时的入射角,由折射定律求解折射角;②根据几何关系求出光线在玻璃砖内通过的路程,由运动学知识求解时间.
【考点精析】利用光的折射对题目进行判断即可得到答案,需要熟知光由一种介质射入另一种介质时,在两种介质的界面上将发生光的传播方向改变的现象叫光的折射.

练习册系列答案
相关题目