Question

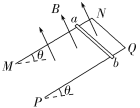
【题目】如图所示，足够长的U形光滑金属导轨平面与水平面成θ角(0<θ<90°)其中MN与PQ平行且间距为L，导轨平面与磁感应强度为B的匀强磁场垂直，导轨电阻不计。金属棒ab由静止开始沿导轨下滑，并与两导轨始终保持垂直且接触良好，ab棒接入电路的电阻为R，当流过ab棒某一横截面的电荷量为q时，棒的速度大小为v，则金属棒ab在这一过程中( )

A．运动的平均速度大小为v

B．下滑的位移大小为

C．产生的焦耳热为qBLv

D．受到的最大安培力大小为sin θ

Answer 1

【答案】B

【解析】分析金属棒的受力情况，有mgsin θ－＝ma，可得金属棒做加速度减小的加速运动，故其平均速度不等于初、末速度的平均值，A错；设金属棒沿斜面下滑的位移为s，则电荷量q＝I·Δt＝··Δt＝＝，解得s＝，B正确；根据能量守恒定律知产生的焦耳热等于金属棒机械能的减少量，Q＝mgssin θ－mv2，C错；金属棒速度越大，安培力越大，所以金属棒受到的最大安培力为，D错。