题目内容
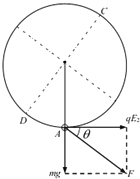
【题目】如图所示，长度为l的绝缘细线将质量为m、电量为q的带正电小球悬挂于O点，整个空间 中充满了匀强电场．（取sin37°＝0.6，cos37°＝0.8）
（1）当电场方向竖直向上时，若使小球在A点获得水平速度
，小球刚好能在竖直平面内做完整的圆周运动，求电场强度E1；
（2）当电场方向水平，且电场强度
时，要不能让细线松弛，求小球在A点获得的水平速度v2应该满足的条件．
【答案】（1）小球刚好能在竖直平面内做完整的圆周运动，电场强度E1应满足
．（2）当电场方向水平，且电场强度
时，要不能让细线松弛，小球在A点获得的水平速度v2应该满足的条件是
或
．
【解析】
（1）当电场力qE1＜mg时，小球在最高点的速度v最小，若小球刚好能通过最高点，
则在最高点有：mg﹣qE1＝m
从最低点到最高点，由动能定理得：﹣（mg﹣qEl）2l＝
解得 
当电场力qE1＞mg时，小球在最低点的速度v最小，若小球刚好能通过最低点，则在最低点有：qE1﹣mg＝m
解得 
联立可得要使小球做完整的圆周运动，电场强度应满足： 
．
（2）当电场方向水平，且时，小球所受重力为mg、电场力qE2的合力大小为
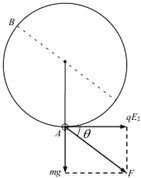
，与水平方向的夹角θ满足tanθ＝
如果小球获得水平速度v2后刚好能做完整的圆周运动，在速度最小的位置B（如图）满足
F＝m
小球从A点运动到B点，由动能定理得：
﹣mgl（1+sinθ）﹣qE2lcosθ＝
联立解得 v2＝
如果小球获得水平速度v2后来回摆动，则小球刚好能到达C点或D点（如上图），则小球从A点运动到C点，由动能定理得：
﹣mgl（1+cosθ）+qE2lsinθ＝0﹣
或小球从A点运动到D点，由动能定理得：
﹣mgl（1﹣cosθ）﹣qE2lsinθ＝0﹣
解得 v2＝
综合可得，v2≥或v2≤细线均不会松驰
黎明文化寒假作业系列答案
