题目内容
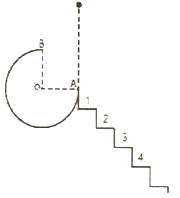
【题目】如图所示，坚直平面内的
圆弧形光滑轨道半径为R=1.6m，A端与圆心0等高，B端 在O的正上方，与A右侧相连的是高和宽都为L=0.3m的台阶，台阶有若干级，一个质量为m=0.3kg的小球从A点正上方h处，由静止释放，自由下落至A点后进入圆形轨道，不计小球进入轨道时的能量损失，不计空气阻力，小球恰能到达轨道的最高点B，求：
（1）释放点距A点的竖直高度；
（2）若释放点距A点的竖直高度H=3R，则小球在B点时对轨道的压力是多大？小球会落在第几级台阶上？设g=10m/s2．
【答案】（1）2.4m（2）9N，第38级台阶上
【解析】试题分析：小球恰能到达轨道的最高点B，由重力提供向心力，由牛顿第二定律求出小球通过B点的速度．对小球从刚释放到B点，由动能定理求释放点距A点的竖直高度．对小球从刚释放到B点，由动能定理求出小球通过B点的速度．在B点，由牛顿定律求小球在B点时对轨道的压力．由平抛运动的规律和几何关系分析小球会落在第几级台阶上．
（1）对小球从刚释放到B点，由动能定理
对小球在B点，由牛顿第二定律
，解得
（2）对小球从刚释放到B点，由动能定理
对小球在B点由牛顿第二定律
，解得
由牛顿第三定律可知，小球在B点对轨道的压力大小是9N．
连接B、A两点并延长，得一倾角为θ的斜面，小球从B点飞出后做平抛运动，设小球经过时间t落到斜面上，水平位移为x，竖直位移为y，落到斜面上时竖直分速度为
，由平抛运动规律，得
， 
由几何关系有
联立解得
所以小球打在第38级台阶上．
练习册系列答案
相关题目
