题目内容
【题目】如图所示,半径r=0.06m的半圆形无场区的圆心在坐标原点O处,半径R=0.1m,磁感应强度大小B=0.075T的圆形有界磁场区的圆心坐标为(0,0.08m),平行金属板MN的极板长L=0.3m、间距d=0.1m,极板间所加电压U=6.4x102V,其中N极板收集到的粒子全部中和吸收。一位于O处的粒子源向第一、二象限均匀地发射速度为v的带正电粒子,经圆形磁场偏转后,从第一象限出射的粒子速度方向均沿x轴正方向,已知粒子在磁场中的运动半径R0=0.08m,若粒子重力不计、比荷![]() =108C/kg、不计粒子间的相互作用力及电场的边缘效应。sin53°=0.8,cos53°=0.6。
=108C/kg、不计粒子间的相互作用力及电场的边缘效应。sin53°=0.8,cos53°=0.6。
(1)求粒子的发射速度v的大小;
(2)若粒子在O点入射方向与x轴负方向夹角为37°,求它打出磁场时的坐标:
(3)N板收集到的粒子占所有发射粒子的比例η。

【答案】(1)6×105m/s;(2)(0,0.18m);(3)29%
【解析】
(1)由洛伦兹力充当向心力,即qvB=m![]()
可得:v=6×105m/s;
(2)若粒子在O点入射方向与x轴负方向夹角为37°,作出速度方向的垂线与y轴交于一点Q,根据几何关系可得PQ=![]() =0.08m,即Q为轨迹圆心的位置;
=0.08m,即Q为轨迹圆心的位置;
Q到圆上y轴最高点的距离为0.18m-![]() =0.08m,故粒子刚好从圆上y轴最高点离开;
=0.08m,故粒子刚好从圆上y轴最高点离开;
故它打出磁场时的坐标为(0,0.18m);
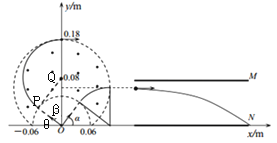
(3)如上图所示,令恰能从下极板右端出射的粒子坐标为y,由带电粒子在电场中偏转的规律得:
y=![]() at2…①
at2…①
a=![]() =
=![]() …②
…②
t=![]() …③
…③
由①②③解得:y=0.08m
设此粒子射入时与x轴的夹角为α,则由几何知识得:y=rsinα+R0-R0cosα
可知tanα=![]() ,即α=53°
,即α=53°
比例η=![]() ×100%=29%
×100%=29%

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目