题目内容
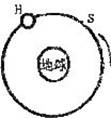
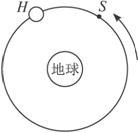
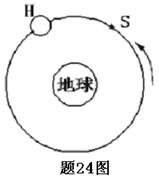
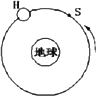
一组太空人乘坐太空穿梭机去修理位于离地球表面h的圆形轨道上的哈勃太空望远镜H,机组人员使穿梭机S进入与H相同的轨道并关闭助推火箭,而望远镜则在穿梭机前方数公里处.如图所示,设G为引力常量而M为地球质量(已知地球半径为R).
(1)在穿梭机内,一质量为m的太空人的视重是多少?
(2)计算轨道上的重力加速度及穿梭机在轨道上的速率和周期;
(3)穿梭机须要想追上望远镜,请你定性分析说明穿梭机该怎么运动.(先说明怎么运动,然后说明理由)
答案:
解析:
解析:
|
(1)穿梭机内的人处于完全失重状态,故视重为零. 4分 (2)由 由 (3)先减速减小半径进入较小的轨道,后加速以较大的角速度追上望远镜.由 |

练习册系列答案
相关题目
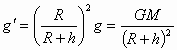 3分
3分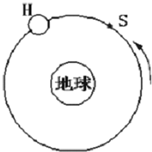 一组太空人乘坐太空穿梭机去修理位于离地球表面h的圆形轨道上的哈勃太空望远镜H,机组人员使穿梭机S进入与H相同的轨道并关闭助推火箭,而望远镜则在穿梭机前方数公里处.如题24图所示,设G为引力常量而M为地球质量(已知地球半径为R).
一组太空人乘坐太空穿梭机去修理位于离地球表面h的圆形轨道上的哈勃太空望远镜H,机组人员使穿梭机S进入与H相同的轨道并关闭助推火箭,而望远镜则在穿梭机前方数公里处.如题24图所示,设G为引力常量而M为地球质量(已知地球半径为R).