题目内容
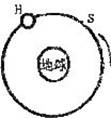
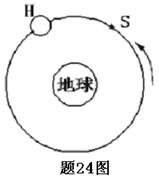
一组太空人乘坐太空穿梭机,去修理位于离地球表面6.0×105 m的圆形轨道上的哈勃太空望远镜H.机组人员使穿梭机S进入与H相同的轨道并关闭助推火箭,而望远镜则在穿梭机前方数千米处.如图5-4-5所示,设G为引力常量而M为地球质量(已知地球半径为6.4×106 m).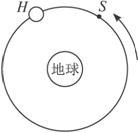
图5-4-5
(1)在穿梭机内,一质量为70 kg的太空人的视重是多少?
(2)计算轨道上的重力加速度及穿梭机在轨道上的速率和周期.
(3)穿梭机须首先进入半径较小的轨道,才有较大的角速度追上望远镜,试判断穿梭机要进入较低轨道时应在原轨道上加速还是减速.说明理由.
思路点拨:本题主要考查万有引力定律在天体运动中的应用.根据万有引力提供向心力,已知轨道半径即可求出速率和周期,根据万有引力近似等于重力,即可求出重力加速度.
解析:(1)穿梭机内的人处于完全失重状态,故视重为零.
(2)由mg=G![]() ,得g=
,得g=![]()
则g′=![]()
![]() =
=![]() =
=![]() =0.84
=0.84
所以g′=0.84g=0.84×9.8 m/s2=8.2 m/s2;
由G![]() =m
=m![]() ,
,
得v=![]() ,v′=
,v′=![]()
![]() =
=![]() =
=![]() =0.96
=0.96
v′=0.96v=0.96×7.9 km/s=7.6 km/s
由v=![]() 得:
得:
T′=![]() =
=![]() s≈5.8×103 s.
s≈5.8×103 s.
(3)由G![]() =m
=m![]() 知穿梭机要进入较低轨道,必须万有引力大于穿梭机做圆周运动所需向心力,故当v减小时,m
知穿梭机要进入较低轨道,必须万有引力大于穿梭机做圆周运动所需向心力,故当v减小时,m![]() 才减小,则G
才减小,则G![]() >m
>m![]() ,使穿梭机的轨道半径减小.
,使穿梭机的轨道半径减小.
答案:(1)零
(2)8.2 m/s2 7.6 km/s 5.8×103 s
(3)减速 理由略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
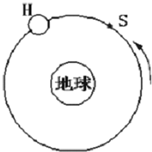 一组太空人乘坐太空穿梭机去修理位于离地球表面h的圆形轨道上的哈勃太空望远镜H,机组人员使穿梭机S进入与H相同的轨道并关闭助推火箭,而望远镜则在穿梭机前方数公里处.如题24图所示,设G为引力常量而M为地球质量(已知地球半径为R).
一组太空人乘坐太空穿梭机去修理位于离地球表面h的圆形轨道上的哈勃太空望远镜H,机组人员使穿梭机S进入与H相同的轨道并关闭助推火箭,而望远镜则在穿梭机前方数公里处.如题24图所示,设G为引力常量而M为地球质量(已知地球半径为R).