题目内容
抛体运动在各类体育运动项目中很常见,如乒乓球运动。现讨论乒乓球发球问题.设球台长2L、网高h,乒乓球反弹前后水平分速度不变,竖直分速度大小不变、方向相反,且不考虑乒乓球的旋转和空气阻力(设重力加速度为g)
若球在球台边缘O点正上方高度为h1处以速度v1水平发出,落在球台的P1点(如图实线所示),求P1点距O点的距离x.;
 若球在O点正上方以速度v2水平发出后.恰好在最高点时越过球网落在球台的P2点(如图虚线所示).求v2的大小.;
若球在O点正上方以速度v2水平发出后.恰好在最高点时越过球网落在球台的P2点(如图虚线所示).求v2的大小.;
(3)若球在O点正上方水平发出后,球经反弹恰好越过球网且刚好落在对方球台边缘P3处,求发球点距O点的高度h3.。
【小题1】![]()
【小题2】![]()
【小题3】![]()
解析:
【小题1】
设发球高度为h1时,球在空中飞行时间为t1,根据平抛运动,有

![]()
![]()
解得:![]()
【小题2】设发球高度为h2,飞行时间为t2,同理根据平抛运动
![]()
![]()
球与球台碰撞后,根据对称性,应有h2=h,2x2=L
得:![]()
【小题3】如图所示,发球高度为h3,飞行时间为t3,同理根据平抛运动

![]()
![]()
球与球台碰撞后,根据对称性,有3x3=2L
设球从恰好越过球网到最高点的时间为t,水平距离为s,有:
![]()
![]()
由几何关系知x3+s=L
联立以上几式,可解得:![]()

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
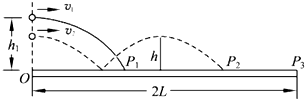 (2008?江苏)抛体运动在各类体育运动项目中很常见,如乒乓球运动.现讨论乒乓球发球问题,设球台长2L、网高h,乒乓球反弹前后水平分速度不变,竖直分速度大小不变、方向相反,且不考虑乒乓球的旋转和空气阻力.(设重力加速度为g)
(2008?江苏)抛体运动在各类体育运动项目中很常见,如乒乓球运动.现讨论乒乓球发球问题,设球台长2L、网高h,乒乓球反弹前后水平分速度不变,竖直分速度大小不变、方向相反,且不考虑乒乓球的旋转和空气阻力.(设重力加速度为g)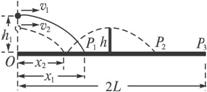
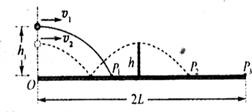 抛体运动在各类体育运动项目中很常见,如乒乓球运动.现讨论乒乓球发球问题,设球台长2L、网高h,乒乓球反弹前后水平分速度不变,竖直分速度大小不变、方向相反,且不考虑乒乓球的旋转和空气阻力.(设重力加速度为g)
抛体运动在各类体育运动项目中很常见,如乒乓球运动.现讨论乒乓球发球问题,设球台长2L、网高h,乒乓球反弹前后水平分速度不变,竖直分速度大小不变、方向相反,且不考虑乒乓球的旋转和空气阻力.(设重力加速度为g)