题目内容
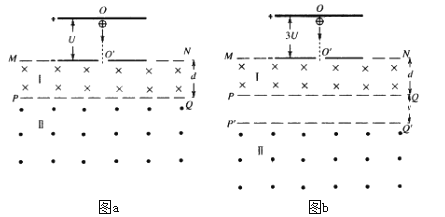
【题目】如图a所示，O为加速电场上极板的中央，下极板中心有一小孔
，O与在同一竖直线上。空间分布着有理想边界的匀强磁场，其边界MN、PQ（加速电场的下极板与边界MN重合）将匀强磁场分为Ⅰ、Ⅱ两个区域，Ⅰ区域高度为d，Ⅱ区域的高度足够大，两个区域的磁感应强度大小相等，方向如图。一个质量为m、电荷量为
的带电粒子从O点由静止释放，经加速后通过小孔，垂直进入磁场Ⅰ区，设加速电场两极板间的电压为U，不计粒子的重力。
（1）求粒子进入磁场Ⅰ区时的速度大小；
（2）若粒子运动一定时间后恰能回到O点，求磁感应强度B的大小；
（3）若将加速电场两极板间的电压提高到
，为使带电粒子运动一定时间后仍能回到O点，需将磁场Ⅱ向下移动一定距离，（如图b所示），求磁场Ⅱ向下移动的距离y及粒子从点进入磁场Ⅰ到第一次回到点的运动时间t。
【答案】（1）
；（2）
；（3）
【解析】
试题分析：（1）粒子在加速电场中做加速运动，由动能定理得：
，解得：；
（2）粒子在磁场中做匀速圆周运动，由牛顿第二定律得：
，
由几何知识得：
，解得：；
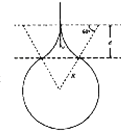
（3）由动能定理得：
，由几何知识得：
，
，
，粒子做圆周运动的时间：
，粒子做匀速直线运动的时间：
，
子从
进入磁场Ⅰ到第一次回到
点的运动时间：
；
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
