Question

【题目】如图所示，ABC为一固定在竖直平面内的光滑轨道，BC段水平，AB段与BC段平滑连接．质量为m的小球从高为h处由静止开始沿轨道下滑，与静止在轨道BC段上质量为km的小球发生碰撞，碰撞前后两小球的运动方向处于同一水平线上．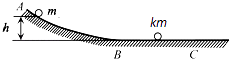

（1）若两小球碰撞后粘连在一起，求碰后它们的共同速度；
（2）若两小球在碰撞过程中无机械能损失，为使两小球能发生第二次碰撞，求k应满足的条件．

Answer 1

【答案】
（1）解：由机械能守恒定律得：

mgh= mv02

设向右为正方向，由动量守恒定律有：

mv0=（m+km）v

v=

答：若两小球碰撞后粘连在一起，碰后它们的共同速度为

（2）解：规定向右为正方向，由动量守恒定律：

mv0=mv1+mv2

得：

根据机械能守恒：

得：

须满足： ＞

得：k＞3

答：若两小球在碰撞过程中无机械能损失，为使两小球能发生第二次碰撞，k应满足的条件k＞3．

【解析】（1）小球下滑过程中机械能守恒，由机械能守恒定律可以求出小球到达水平面的速度；两球碰撞过程动量守恒，由动守恒定律可以求出两球的共同速度．（2）分析出两球第二次碰撞的条件，应用动量守恒定律与机械能守恒定律分析答题．