题目内容
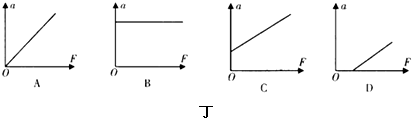
1.一个弹簧振子沿x轴做简谐运动,取平衡位置O为x轴坐标原点.从某时刻开始计时,经过四分之一周期,振子具有沿x轴正方向的最大加速度.能正确反映振子位移x与时间t关系的图象是( )| A. |  | B. |  | C. |  | D. | 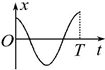 |
分析 根据从某时刻开始计时,经过四分之一周期,振子具有沿x轴正方向的最大加速度,由a=-$\frac{kx}{m}$分析四分之一周期时刻振子的位移,即可知道t=0时刻质点的位移,确定位移的图象.
解答 解:根据简谐运动的特征:a=-$\frac{kx}{m}$,可知,经过四分之一周期,振子具有沿x轴正方向的最大加速度,则此时振子的位移为负向最大,计时起点时,位移为正向最大,故A正确.
故选:A
点评 本题在选择图象时,关键研究t=0时刻质点的位移和位移如何变化,要掌握简谐运动的特征:a=-$\frac{kx}{m}$,分析加速度和位移的关系.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
12.若一个台秤放在电梯里的地面上,台秤上放一个重为G的物体,以下说法正确的是( )
| A. | 电梯减速上升时,物体受到的支持力大于物体对台秤的压力 | |
| B. | 电梯匀速上升时,物体受到的支持力等于物体对台秤的压力 | |
| C. | 加速上升时,物体受到的重力大于G | |
| D. | 减速下降时,台秤的示数小于G |
9.将质量为m的滑块放在倾角为θ的固定斜面上.滑块与斜面之间的动摩擦因数为μ.若滑块与斜面之间的最大静摩擦力和滑动摩擦力大小相等,重力加速度为g,则( )
| A. | 将滑块由静止释放,如果μ>tanθ,滑块将下滑 | |
| B. | 给滑块沿斜面向下的初速度,如果μ<tanθ,滑块将减速下滑 | |
| C. | 用平行于斜面向上的力拉滑块向上匀速滑动,如果μ=tanθ,拉力大小应是2mgsinθ | |
| D. | 用平行于斜面向下的力拉滑块向下匀速滑动,如果μ=tanθ,拉力大小应是mgsinθ |
6.LC电路中电容器极板上的电荷量随时间的变化关系如图所示,下列说法中错误的是( )
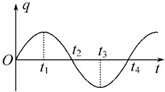

| A. | 在t1时刻,电路中的磁场能最小 | |
| B. | 从t1时刻到t2时刻,电路中电流变小 | |
| C. | 从t2时刻到t3时刻,电容器充电 | |
| D. | 在t4时刻,电容器的电场能最小 |
13.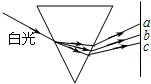 如图所示,一细束白光通过玻璃三棱镜折射后分为各种单色光,取其中a、b、c三种色光,下列说法正确的是( )
如图所示,一细束白光通过玻璃三棱镜折射后分为各种单色光,取其中a、b、c三种色光,下列说法正确的是( )
 如图所示,一细束白光通过玻璃三棱镜折射后分为各种单色光,取其中a、b、c三种色光,下列说法正确的是( )
如图所示,一细束白光通过玻璃三棱镜折射后分为各种单色光,取其中a、b、c三种色光,下列说法正确的是( )| A. | c光的频率最高 | B. | 在真空中c光的波长最长 | ||
| C. | 玻璃对c光的折射率最大 | D. | 在三棱镜中的c光传播速度最小 |
10. 如图所示,弹性金属铜环A、B的面积相等(略大于磁铁的截面),环A是闭合的,环B在底端有个小缺口,缺口处用绝缘物质密封,横梁可以绕中间的支点转动.开始时整个装置静止,用磁铁的任意一极分别去接近环A或B,则( )
如图所示,弹性金属铜环A、B的面积相等(略大于磁铁的截面),环A是闭合的,环B在底端有个小缺口,缺口处用绝缘物质密封,横梁可以绕中间的支点转动.开始时整个装置静止,用磁铁的任意一极分别去接近环A或B,则( )
 如图所示,弹性金属铜环A、B的面积相等(略大于磁铁的截面),环A是闭合的,环B在底端有个小缺口,缺口处用绝缘物质密封,横梁可以绕中间的支点转动.开始时整个装置静止,用磁铁的任意一极分别去接近环A或B,则( )
如图所示,弹性金属铜环A、B的面积相等(略大于磁铁的截面),环A是闭合的,环B在底端有个小缺口,缺口处用绝缘物质密封,横梁可以绕中间的支点转动.开始时整个装置静止,用磁铁的任意一极分别去接近环A或B,则( )| A. | 靠近A时,A将后退且扩张 | |
| B. | 靠近A时,A将后退且收缩 | |
| C. | 靠近A或B时,相应的环中产生感应电动势 | |
| D. | 靠近A或B时,相应的环中一定产生感应电流 |
11. 如图,光滑斜面的倾角为θ,斜面上放置一矩形导体线框abcd,ab边的边长为l1,bc边的边长为l2,线框的质量为m、电阻为R,线框通过绝缘细线绕过光滑的小滑轮与重物相连,重物质量为M,斜面上ef线(ef平行底边)的右上方有垂直斜面向上的匀强磁场,磁感应强度为B,如果线框从静止开始运动,进入磁场的最初一段时间是做匀速运动的,且线框的ab边始终平行底边,则下列说法正确的是( )
如图,光滑斜面的倾角为θ,斜面上放置一矩形导体线框abcd,ab边的边长为l1,bc边的边长为l2,线框的质量为m、电阻为R,线框通过绝缘细线绕过光滑的小滑轮与重物相连,重物质量为M,斜面上ef线(ef平行底边)的右上方有垂直斜面向上的匀强磁场,磁感应强度为B,如果线框从静止开始运动,进入磁场的最初一段时间是做匀速运动的,且线框的ab边始终平行底边,则下列说法正确的是( )
 如图,光滑斜面的倾角为θ,斜面上放置一矩形导体线框abcd,ab边的边长为l1,bc边的边长为l2,线框的质量为m、电阻为R,线框通过绝缘细线绕过光滑的小滑轮与重物相连,重物质量为M,斜面上ef线(ef平行底边)的右上方有垂直斜面向上的匀强磁场,磁感应强度为B,如果线框从静止开始运动,进入磁场的最初一段时间是做匀速运动的,且线框的ab边始终平行底边,则下列说法正确的是( )
如图,光滑斜面的倾角为θ,斜面上放置一矩形导体线框abcd,ab边的边长为l1,bc边的边长为l2,线框的质量为m、电阻为R,线框通过绝缘细线绕过光滑的小滑轮与重物相连,重物质量为M,斜面上ef线(ef平行底边)的右上方有垂直斜面向上的匀强磁场,磁感应强度为B,如果线框从静止开始运动,进入磁场的最初一段时间是做匀速运动的,且线框的ab边始终平行底边,则下列说法正确的是( )| A. | 线框进入磁场前运动的加速度为$\frac{Mg-mgsinθ}{M+m}$ | |
| B. | 线框进入磁场时匀速运动的速度为$\frac{(Mg-mgsinθ)R}{{{B^2}l_2^2}}$ | |
| C. | 线框进入磁场时做匀速运动的总时间为$\frac{{{B^2}l_1^2{l_2}}}{(Mg-mgsinθ)R}$ | |
| D. | 若该线框进入磁场时做匀速运动,则匀速运动过程产生的焦耳热为(Mg-mgsinθ)l2 |
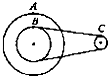 如图,A、B、C三轮半径之比为3:2:1,A与B共轴,B与C用不打滑的皮带轮传动,则A、B、C三轮的轮缘上各点的线速度大小之比为3:2:2,角速度大小之比为1:1:2,转动的向心加速度大小之比为3:2:4.
如图,A、B、C三轮半径之比为3:2:1,A与B共轴,B与C用不打滑的皮带轮传动,则A、B、C三轮的轮缘上各点的线速度大小之比为3:2:2,角速度大小之比为1:1:2,转动的向心加速度大小之比为3:2:4.