��Ŀ����
11�� ��ͼ���⻬б������Ϊ�ȣ�б���Ϸ���һ���ε����߿�abcd��ab�ߵı߳�Ϊl1��bc�ߵı߳�Ϊl2���߿������Ϊm������ΪR���߿�ͨ����Եϸ���ƹ��⻬��С������������������������ΪM��б����ef�ߣ�efƽ�еױߣ������Ϸ��д�ֱб�����ϵ���ǿ�ų����Ÿ�Ӧǿ��ΪB������߿�Ӿ�ֹ��ʼ�˶�������ų������һ��ʱ�����������˶��ģ����߿��ab��ʼ��ƽ�еױߣ�������˵����ȷ���ǣ�������
��ͼ���⻬б������Ϊ�ȣ�б���Ϸ���һ���ε����߿�abcd��ab�ߵı߳�Ϊl1��bc�ߵı߳�Ϊl2���߿������Ϊm������ΪR���߿�ͨ����Եϸ���ƹ��⻬��С������������������������ΪM��б����ef�ߣ�efƽ�еױߣ������Ϸ��д�ֱб�����ϵ���ǿ�ų����Ÿ�Ӧǿ��ΪB������߿�Ӿ�ֹ��ʼ�˶�������ų������һ��ʱ�����������˶��ģ����߿��ab��ʼ��ƽ�еױߣ�������˵����ȷ���ǣ�������| A�� | �߿����ų�ǰ�˶��ļ��ٶ�Ϊ$\frac{Mg-mgsin��}{M+m}$ | |
| B�� | �߿����ų�ʱ�����˶����ٶ�Ϊ$\frac{��Mg-mgsin�ȣ�R}{{{B^2}l_2^2}}$ | |
| C�� | �߿����ų�ʱ�������˶�����ʱ��Ϊ$\frac{{{B^2}l_1^2{l_2}}}{��Mg-mgsin�ȣ�R}$ | |
| D�� | �����߿����ų�ʱ�������˶����������˶����̲����Ľ�����Ϊ��Mg-mgsin�ȣ�l2 |
���� �߿����ų�ǰ������ţ�ٵڶ����������ٶȣ��߿����ų��Ĺ����������˶���M���������ܼ�Сת��Ϊm���������ܺ��߿��е����ܣ����������غ㶨����⽹���ȣ���ƽ����������߿������˶����ٶȣ������ʱ�䣮
��� �⣺A���߿����ų�ǰ�������壬����ţ�ٵڶ����ɵã��߿�ļ��ٶ�Ϊa=$\frac{Mg-mgsin��}{M+m}$����A��ȷ��
B��C���߿������˶����ٶȴ�СΪv�����߿��ܵ��İ�������СΪF=$\frac{{B}^{2}{l}_{1}^{2}v}{R}$�����߿���ƽ�������ã�F=Mg-mgsin�ȣ�������ʽ�ã�v=$\frac{Mg-mgsin��}{{B}^{2}{l}_{1}^{2}}R$�������˶���ʱ��Ϊ
t=$\frac{{l}_{2}}{v}$=$\frac{{B}^{2}{l}_{1}^{2}{l}_{2}}{��Mg-mgsin�ȣ�R}$����B����C��ȷ��
D���߿����ų��Ĺ����������˶���M���������ܼ�Сת��Ϊm���������ܺ��߿��е����ܣ����������غ㶨�ɵã������˶����̲����Ľ�����ΪQ=��Mg-mgsin�ȣ�l2����D��ȷ��
��ѡ��ACD��
���� �����ǵ�Ÿ�Ӧ����ƽ����ۺϣ��������ļ����ǹؼ������������õ������巨�����ٶȣ�

��ϰ��ϵ�д�
�����Ŀ
6������˵������ȷ���ǣ�������
| A�� | ���е������غ���̶����Է��ط��� | |
| B�� | �ȴ��ݡ�Ħ�����Ⱥ������������Ͷ��ǿ������ | |
| C�� | �������ж�����ʽ��������ú��ʯ�͡������ܵȶ�����̫����������� | |
| D�� | �ܵ�ת�����̷��������غ㶨�ɣ���˲��ᷢ����ԴΣ�� |
3��������ѧ��չ�Ĺ����У���������ѧ�ҵĿ�ѧ�����ƶ���������ʷ�Ľ����������¼�λ����ѧ��������ѧ���ı����У�����ʵ������ǣ�������
| A�� | ��������������˵����������������Բ������еĹ��� | |
| B�� | ������ͨ���о����ǹ۲��¼�������������˶������� | |
| C�� | �ѿ�����������б��ʵ�飬�����������ά�������˶���ԭ�� | |
| D�� | ţ�����Ƚ�ʵ����ʵ����������������ѧ���ݣ���г�ؽ������ |




 ��ͼ��ʾ��Ϊһ�����¶ȼƵĽṹʾ��ͼ������һ��������������IJ�����Pͨ��ϸ����ˮ��ѹǿ�����A������ѹǿ���ҹ�B��C�������ͨ���ƶ��ҹ�B�ɵ�����ˮ����ĸ߶ȣ��Ӷ���֤��������������䣮��������P���ڱ�ˮ������С�����ѹǿ�൱��76cm��ˮ������������ѹǿʱ��ѹǿ���������ܵ�ˮ����ǡ�ö�λ��ͼʾ�̶ȳߵ���̶ȴ���
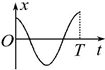
��ͼ��ʾ��Ϊһ�����¶ȼƵĽṹʾ��ͼ������һ��������������IJ�����Pͨ��ϸ����ˮ��ѹǿ�����A������ѹǿ���ҹ�B��C�������ͨ���ƶ��ҹ�B�ɵ�����ˮ����ĸ߶ȣ��Ӷ���֤��������������䣮��������P���ڱ�ˮ������С�����ѹǿ�൱��76cm��ˮ������������ѹǿʱ��ѹǿ���������ܵ�ˮ����ǡ�ö�λ��ͼʾ�̶ȳߵ���̶ȴ��� һ����x���������ļ��Შ��t=0ʱ�̵IJ�����ͼ��ʾ���ʵ�P��x����Ϊ3m����֪�������ʵ�����2�ξ���ƽ��λ�õ�ʱ����Ϊ0.4s������Ϊ5m/s��x������Ϊ22m���ʵ���t=0.2sʱǡ��λ�ڲ��壨����/���ȣ�
һ����x���������ļ��Შ��t=0ʱ�̵IJ�����ͼ��ʾ���ʵ�P��x����Ϊ3m����֪�������ʵ�����2�ξ���ƽ��λ�õ�ʱ����Ϊ0.4s������Ϊ5m/s��x������Ϊ22m���ʵ���t=0.2sʱǡ��λ�ڲ��壨����/���ȣ�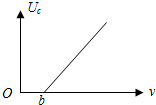 ��ij���ЧӦʵ���У��õ��Ķ�ֹ��ѹUc��������Ƶ��v�Ĺ�ϵ��ͼ��ʾ������ֱ�ߵ�б��Ϊk������ؾ�Ϊb�����ӵ�����ľ���ֵΪe����
��ij���ЧӦʵ���У��õ��Ķ�ֹ��ѹUc��������Ƶ��v�Ĺ�ϵ��ͼ��ʾ������ֱ�ߵ�б��Ϊk������ؾ�Ϊb�����ӵ�����ľ���ֵΪe����