题目内容
某实验小组在利用单摆测定当地重力加速度的实验中：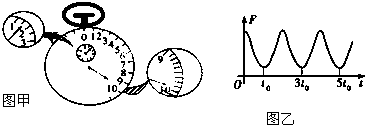
（1）然后用秒表记录了单摆振动所用的时间如图甲所示，则秒表读数为
（2）接着测量了摆线的长度为l0，小球的直直径为d，实验时用拉力传感器测得摆线的拉力F随时间t变化的图象如图乙所示，则重力加速度的表达式g=
（用题目中的物理量表示）．
（3）某小组改变摆线长度l0，测量了多组数据．在进行数据处理时，甲同学把摆线长l0作为摆长，直接利用公式求出各组重力加速度值再求出平均值；乙同学作出T2-l0图象后求出斜率，然后算出重力加速度．两同学处理数据的方法对结果的影响是：甲
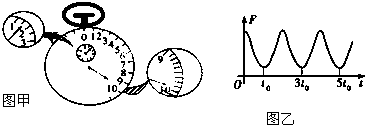
（1）然后用秒表记录了单摆振动所用的时间如图甲所示，则秒表读数为
99.8
99.8
s．（2）接着测量了摆线的长度为l0，小球的直直径为d，实验时用拉力传感器测得摆线的拉力F随时间t变化的图象如图乙所示，则重力加速度的表达式g=
π2(l0+
| ||
4
|
π2(l0+
| ||
4
|
（3）某小组改变摆线长度l0，测量了多组数据．在进行数据处理时，甲同学把摆线长l0作为摆长，直接利用公式求出各组重力加速度值再求出平均值；乙同学作出T2-l0图象后求出斜率，然后算出重力加速度．两同学处理数据的方法对结果的影响是：甲
偏小
偏小
，乙无影响
无影响
．（填“偏大”、“偏小”或“无影响”）分析：秒表中间的表盘代表分钟，周围的大表盘代表秒，秒表读数是两个表盘的示数之和，要注意观察指针所指的位置及分度值；
单摆的摆长等于摆线的长度与摆球的半径之和，根据题意求出摆长，摆球在最大位移处摆线的拉力最小，在最低点处，摆线的拉力最大，摆球从最大位移处，经最低点到达另一测最大位移处，然后再次反向通过最低点，最后回到最初的位置，经历的时间是一个周期，摆线的拉力经历三个最小值，由图乙所示图象求出单摆的周期T；最后由单摆周期公式求出重力加速度的表达式．
根据单摆周期公式判断甲的测量值与真实值间的关系；由单摆周期公式的变形公式求出T2-L关系表达式，然后根据图象求出重力加速度，然后判断测量值与真实值间的关系．
单摆的摆长等于摆线的长度与摆球的半径之和，根据题意求出摆长，摆球在最大位移处摆线的拉力最小，在最低点处，摆线的拉力最大，摆球从最大位移处，经最低点到达另一测最大位移处，然后再次反向通过最低点，最后回到最初的位置，经历的时间是一个周期，摆线的拉力经历三个最小值，由图乙所示图象求出单摆的周期T；最后由单摆周期公式求出重力加速度的表达式．
根据单摆周期公式判断甲的测量值与真实值间的关系；由单摆周期公式的变形公式求出T2-L关系表达式，然后根据图象求出重力加速度，然后判断测量值与真实值间的关系．
解答：解：（1）图示秒表内圈示数是1.5min=90s，外圈示数是9.8s，秒表所示是90s+9.8s=99.8s；
（2）单摆摆长等于摆线长度与摆球半径之和，即单摆摆长：L=l0+
由图乙所示图象可知，单摆的周期：T=5t0-t0=4t0，
单摆周期公式：T=2π
得：g=
=
（3）由单摆周期公式T=2π
可知，重力加速度g=
，摆长应该是摆线长度与摆球半径之和，
甲同学把摆线长L作为摆长，摆长小于实际摆长，由g=
可知，重力加速度的测量值小于真实值；
由T=2π
可知，L=
=kT2其中k=
由此可见，L与T2成正比，k是比例常数；
由于单摆摆长偏大还是偏小不影响图象的斜率k，因此摆长偏小不影响重力加速度的测量值
故答案为：99.8，
，偏小，无影响
（2）单摆摆长等于摆线长度与摆球半径之和，即单摆摆长：L=l0+
| d |
| 2 |
由图乙所示图象可知，单摆的周期：T=5t0-t0=4t0，
单摆周期公式：T=2π
|
| 4π2L |
| T2 |
π2(l0+
| ||
4
|
（3）由单摆周期公式T=2π
|
| 4π2L |
| T2 |
甲同学把摆线长L作为摆长，摆长小于实际摆长，由g=
| 4π2L |
| T2 |
由T=2π
|
| gT2 |
| 4π2 |
| g |
| 4π2 |
由于单摆摆长偏大还是偏小不影响图象的斜率k，因此摆长偏小不影响重力加速度的测量值
故答案为：99.8，
π2(l0+
| ||
4
|
点评：根据图乙所示图象求出单摆的周期是易错点，要掌握单摆的运动过程，结合图象求出单摆周期；熟练应用单摆周期公式是正确解题的关键
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
某实验小组在利用单摆测定当地重力加速度的实验中：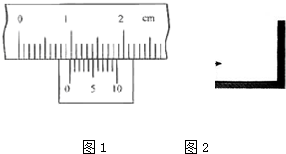
（1）碘131核不稳定，会发生β衰变，其半衰变期为8天．碘131核的衰变方程：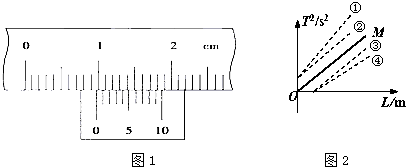
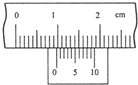（2011?福建）（1）某实验小组在利用单摆测定当地重力加速度的实验中：