题目内容
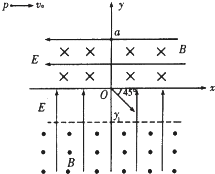
如图所示,在y轴竖直向上的直角坐标系中,电场、磁场的分布情况如下:①在o<y<α口的区域内,存在沿x轴负向的匀强电场和垂直xoy平面向里的匀强磁场;
②在y<o区域内,存在沿y轴正向的匀强电场;
③在y<y1区域内,同时存在垂直xoy平面向外的匀强磁场;
各区域的电场、磁场强弱相同.一质量为m、电量为q带正电的小球,从xoy平面内的P点以初速v向右抛出.小球进入0<y<α的复合场区沿直线运动,恰好过坐标原点,方向如图.如果小球能够第二次到达O点,m、α、v、q、g为已知量,求:
(1)p点坐标;
(2)磁感应强度B;
(3)小球两次通过O点经历的时间.

【答案】分析:(1)小球从P点抛出后先做平抛运动,进入复合场后做匀速直线运动,由于小球恰好通过原点O,且速度方向与x轴成45°,运用运动的分解法可求得小球刚进入复合场时的竖直分速度与水平分速度相等,由运动学公式即可求得P点的坐标.
(2)小球在0<y<α区域沿直线运动,一定是匀速直线运动,合力为零,作出力图,由平衡条件和洛伦兹力公式列式,可求得B.
(3)小球在y<0区域内运动如图丙所示,先作匀速直线运动,后作匀速圆周运动,再做直线运动至O点,分段求时间,即可求得总时间.磁场中,由牛顿第二定律和圆周运动公式求得周期,根据轨迹的圆心角求时间.
解答:解:(1)带电小球进入0<y<α区域时,速度方向如图甲,
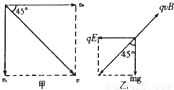
由此可知,vy=v
小球由P点抛出做平抛运动.
vy=gt
由①②可得t=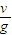
所以,水平位移s=vt=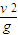
垂直位移h=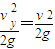
由小球沿直线运动可知,小球进入此区域时的坐标为(-α,α).
故P点坐标为[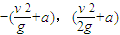 ]⑤
]⑤
(2)小球在0<y<α区域沿直线运动,一定是匀速直线运动,受力如图乙所示
qE=mg ⑥
由qvB=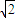 mg和v=
mg和v=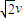 ⑦
⑦
解得B=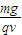 ⑧
⑧
(3)小球在y<0区域内运动如图丙所示,先作匀速直线运动,后作匀速圆周运动,再做直线运动至O点,设其运动时间分别为t1、t2、t3,⑨
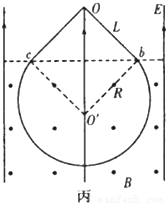
由Loc=Lob=R,qvB=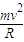 ,和Lob=vt1 ⑩
,和Lob=vt1 ⑩
得t1=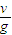 (11)
(11)
T=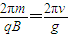 (12)
(12)
t2= (13)
(13)
分析知t3=t1=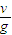 ,两次经过O点历时间为
,两次经过O点历时间为
t=2t1+t2=(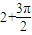 )
)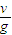 (14)
(14)
答:
(1)P点坐标为[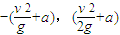 ].
].
(2)磁感应强度B是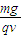 ;
;
(3)小球两次通过O点经历的时间为(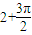 )
)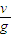 .
.
点评:对于带电粒子在电磁场中运动的问题,应运用力学的基本方法分析粒子的受力情况,确定其运动情况,再选择相应的物理规律求解.
(2)小球在0<y<α区域沿直线运动,一定是匀速直线运动,合力为零,作出力图,由平衡条件和洛伦兹力公式列式,可求得B.
(3)小球在y<0区域内运动如图丙所示,先作匀速直线运动,后作匀速圆周运动,再做直线运动至O点,分段求时间,即可求得总时间.磁场中,由牛顿第二定律和圆周运动公式求得周期,根据轨迹的圆心角求时间.
解答:解:(1)带电小球进入0<y<α区域时,速度方向如图甲,

由此可知,vy=v
小球由P点抛出做平抛运动.
vy=gt
由①②可得t=
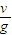
所以,水平位移s=vt=
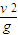
垂直位移h=
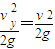
由小球沿直线运动可知,小球进入此区域时的坐标为(-α,α).
故P点坐标为[
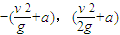 ]⑤
]⑤(2)小球在0<y<α区域沿直线运动,一定是匀速直线运动,受力如图乙所示
qE=mg ⑥
由qvB=
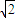 mg和v=
mg和v=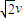 ⑦
⑦解得B=
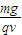 ⑧
⑧(3)小球在y<0区域内运动如图丙所示,先作匀速直线运动,后作匀速圆周运动,再做直线运动至O点,设其运动时间分别为t1、t2、t3,⑨

由Loc=Lob=R,qvB=
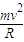 ,和Lob=vt1 ⑩
,和Lob=vt1 ⑩得t1=
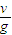 (11)
(11)T=
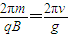 (12)
(12)t2=
 (13)
(13)分析知t3=t1=
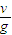 ,两次经过O点历时间为
,两次经过O点历时间为t=2t1+t2=(
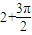 )
)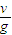 (14)
(14)答:
(1)P点坐标为[
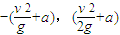 ].
].(2)磁感应强度B是
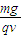 ;
;(3)小球两次通过O点经历的时间为(
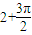 )
) .
.点评:对于带电粒子在电磁场中运动的问题,应运用力学的基本方法分析粒子的受力情况,确定其运动情况,再选择相应的物理规律求解.

练习册系列答案
相关题目
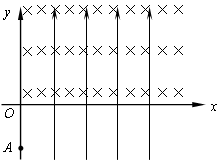
 在xoy竖直平面内,仅在第一、四象限分布着竖直向上的匀强电场E,第一象限还存在着垂直纸面向里的匀强磁场B,方向如图所示.在y轴负向A点处有一质量为1.0×10-6 kg,电量为q=1.0×10-6 c的带正电微粒以初速度v0=8m/s,垂直y轴射入第四象限内.其中电场强度E=20N/c,OA的长为d=1.8m,g取10m/s2.
在xoy竖直平面内,仅在第一、四象限分布着竖直向上的匀强电场E,第一象限还存在着垂直纸面向里的匀强磁场B,方向如图所示.在y轴负向A点处有一质量为1.0×10-6 kg,电量为q=1.0×10-6 c的带正电微粒以初速度v0=8m/s,垂直y轴射入第四象限内.其中电场强度E=20N/c,OA的长为d=1.8m,g取10m/s2.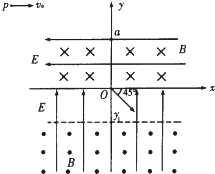 如图所示,在y轴竖直向上的直角坐标系中,电场、磁场的分布情况如下:
如图所示,在y轴竖直向上的直角坐标系中,电场、磁场的分布情况如下: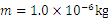 ,电量为
,电量为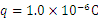 的带正电微粒以初速度
的带正电微粒以初速度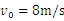 ,垂直y轴射入第四象限内。其中电场强度
,垂直y轴射入第四象限内。其中电场强度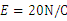 ,OA的长为
,OA的长为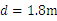 ,g取
,g取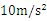 。
。
 ;
;