��Ŀ����
��ͼ��ʾ����y����ֱ���ϵ�ֱ������ϵ�У��糡���ų��ķֲ�������£�
����o��y�����ڵ������ڣ�������x�Ḻ�����ǿ�糡�ʹ�ֱxoyƽ���������ǿ�ų���
����y��o�����ڣ�������y���������ǿ�糡��
����y��y1�����ڣ�ͬʱ���ڴ�ֱxoyƽ���������ǿ�ų���
������ĵ糡���ų�ǿ����ͬ��һ����Ϊm������Ϊq�������С��xoyƽ���ڵ�P���Գ���v0�����׳���С�����0��y�����ĸ��ϳ�����ֱ���˶���ǡ�ù�����ԭ�㣬������ͼ�����С���ܹ��ڶ��ε���O�㣬m������v0��q��gΪ��֪������
��1��p�����ꣻ
��2���Ÿ�Ӧǿ��B��
��3��С������ͨ��O�㾭����ʱ�䣮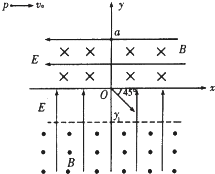
����o��y�����ڵ������ڣ�������x�Ḻ�����ǿ�糡�ʹ�ֱxoyƽ���������ǿ�ų���
����y��o�����ڣ�������y���������ǿ�糡��
����y��y1�����ڣ�ͬʱ���ڴ�ֱxoyƽ���������ǿ�ų���
������ĵ糡���ų�ǿ����ͬ��һ����Ϊm������Ϊq�������С��xoyƽ���ڵ�P���Գ���v0�����׳���С�����0��y�����ĸ��ϳ�����ֱ���˶���ǡ�ù�����ԭ�㣬������ͼ�����С���ܹ��ڶ��ε���O�㣬m������v0��q��gΪ��֪������
��1��p�����ꣻ
��2���Ÿ�Ӧǿ��B��
��3��С������ͨ��O�㾭����ʱ�䣮

��1������С�����0��y��������ʱ���ٶȷ�����ͼ�ף�
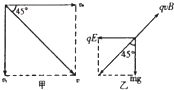
�ɴ˿�֪��vy=v0
С����P���׳���ƽ���˶���
vy=gt
�ɢ٢ڿɵ�t=
���ԣ�ˮƽλ��s=v0t=
��ֱλ��h=
=
��С����ֱ���˶���֪��С����������ʱ������Ϊ��-����������
��P������Ϊ[-(
+a)��(
+a)]��
��2��С����0��y����������ֱ���˶���һ��������ֱ���˶���������ͼ����ʾ
qE=mg ��
��qvB=
mg��v=
v0��
���B=
��
��3��С����y��0�������˶���ͼ����ʾ����������ֱ���˶�����������Բ���˶�������ֱ���˶���O�㣬�����˶�ʱ��ֱ�Ϊt1��t2��t3����
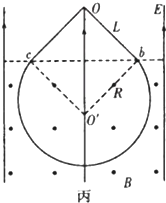
��Loc=Lob=R��qvB=
����Lob=vt1 ��
��t1=
��11��
T=
=
��12��
t2=
t=
��13��
����֪t3=t1=
�����ξ���O����ʱ��Ϊ
t=2t1+t2=��2+
��
��14��
��
��1��P������Ϊ[-(
+a)��(
+a)]��
��2���Ÿ�Ӧǿ��B��
��
��3��С������ͨ��O�㾭����ʱ��Ϊ��2+
��
��

�ɴ˿�֪��vy=v0
С����P���׳���ƽ���˶���
vy=gt
�ɢ٢ڿɵ�t=
| v0 |
| g |
���ԣ�ˮƽλ��s=v0t=
| ||
| g |
��ֱλ��h=
| ||
| 2g |
| ||
| 2g |
��С����ֱ���˶���֪��С����������ʱ������Ϊ��-����������
��P������Ϊ[-(
| ||
| g |
| ||
| 2g |
��2��С����0��y����������ֱ���˶���һ��������ֱ���˶���������ͼ����ʾ
qE=mg ��
��qvB=
| 2 |
| 2 |
���B=
| mg |
| qv0 |
��3��С����y��0�������˶���ͼ����ʾ����������ֱ���˶�����������Բ���˶�������ֱ���˶���O�㣬�����˶�ʱ��ֱ�Ϊt1��t2��t3����

��Loc=Lob=R��qvB=
| mv2 |
| R |
��t1=
| v0 |
| g |
T=
| 2��m |
| qB |
| 2��v0 |
| g |
t2=
| 3 |
| 4 |
| 3��v0 |
| 2g |
����֪t3=t1=
| v0 |
| g |
t=2t1+t2=��2+
| 3�� |
| 2 |
| v0 |
| g |
��
��1��P������Ϊ[-(
| ||
| g |
| ||
| 2g |
��2���Ÿ�Ӧǿ��B��
| mg |
| qv0 |
��3��С������ͨ��O�㾭����ʱ��Ϊ��2+
| 3�� |
| 2 |
| v0 |
| g |

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
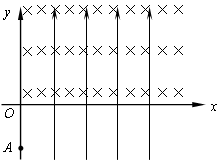
 ��xoy��ֱƽ���ڣ����ڵ�һ�������ֲ�����ֱ���ϵ���ǿ�糡E����һ���������Ŵ�ֱֽ���������ǿ�ų�B��������ͼ��ʾ����y�Ḻ��A�㴦��һ����Ϊ1.0��10-6 kg������Ϊq=1.0��10-6 c�Ĵ��������Գ��ٶ�v0=8m/s����ֱy��������������ڣ����е糡ǿ��E=20N/c��OA�ij�Ϊd=1.8m��gȡ10m/s2��
��xoy��ֱƽ���ڣ����ڵ�һ�������ֲ�����ֱ���ϵ���ǿ�糡E����һ���������Ŵ�ֱֽ���������ǿ�ų�B��������ͼ��ʾ����y�Ḻ��A�㴦��һ����Ϊ1.0��10-6 kg������Ϊq=1.0��10-6 c�Ĵ��������Գ��ٶ�v0=8m/s����ֱy��������������ڣ����е糡ǿ��E=20N/c��OA�ij�Ϊd=1.8m��gȡ10m/s2��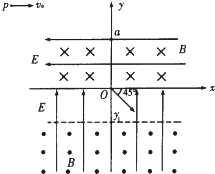 ��ͼ��ʾ����y����ֱ���ϵ�ֱ������ϵ�У��糡���ų��ķֲ�������£�
��ͼ��ʾ����y����ֱ���ϵ�ֱ������ϵ�У��糡���ų��ķֲ�������£�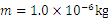 ������Ϊ
������Ϊ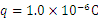 �Ĵ��������Գ��ٶ�
�Ĵ��������Գ��ٶ�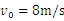 ����ֱy��������������ڡ����е糡ǿ��
����ֱy��������������ڡ����е糡ǿ��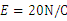 ��OA�ij�Ϊ
��OA�ij�Ϊ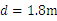 ��gȡ
��gȡ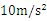 ��
��
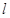 ��
��