题目内容
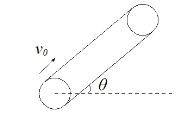
【题目】在光滑水平面上放置两长度相同、质量分别为m1和m2的木板P、Q，在木板的左端各有一大小、形状、质量完全相同的物块a和b，木板和物块均处于静止状态。现对物块a和b分别施加水平恒力F1和F2，使它们向右运动。当物块与木板分离时，P、Q的速度分别为v1、v2，物块P、Q相对地面的位移分别为s1、s2。已知两物块与木板间的动摩擦因数相同，下列判断正确的是 ( )
A.若F1＝F2、m1>m2，则V1<V2、S1<S2
B.若F1＝F2、m1<m2，则
、S1<S2
C.若F1 > F2、m1=m2，则
、
D.若F1 < F2、m1=m2，则、
【答案】AD
【解析】
A、首先看F1=F2时情况：
由题很容易得到a、b 所受的摩擦力大小是相等的，因此a、b 加速度相同，我们设a、b 加速度大小为a，
对于P、Q，滑动摩擦力即为它们的合力，设P（m1）的加速度大小为a1，Q（m2）的加速度大小为a2，
根据牛顿第二定律得：
因为
，其中m为物块a和b的质量．
设板的长度为L，它们向右都做匀加速直线运动，当物块与木板分离时：
a与P 的相对位移
b与Q 的相对位移
若m1＞m2，a1＜a2
所以得：t1＜t2
P的速度为v1=a1t1，Q的速度为v2=a2t2
物块a相对地面的位移分别为
物块b相对地面的位移分别为
则v1＜v2，s1＜s2，故A正确，B错误．
C、若F1＞F2、m1=m2，根据受力分析和牛顿第二定律的：
则a的加速度大于b的加速度，即aa＞ab
由于m1=m2，所以P、Q加速度相同，设P、Q加速度为a．
它们向右都做匀加速直线运动，当物块与木板分离时：
a与P 的相对位移
b与Q 的相对位移
由于aa＞ab，所以得：t1＜t2，则v1＜v2，s1＜s2，故C错误．
D、根据C选项分析得：若F1＜F2、m1=m2，aa＜ab，则v1＞v2、S1＞S2，故D正确．
故选AD．
