题目内容
如图甲,质量为m的小木块左端与轻弹簧相连,弹簧的另一端与固定在足够大的光滑水平桌面上的挡板相连,木块的右端与一轻细线连接,细线绕过光滑的质量不计的轻滑轮,木块处于静止状态.在下列情况中弹簧均处于弹性限度内,不计空气阻力及线的形变,重力加速度为g.
(1)图甲中,在线的另一端施加一竖直向下的大小为F的恒力,木块离开初始位置O由静止开始向右运动,弹簧开始发生伸长形变,已知木块过P点时,速度大小为v,O、P两点间距离为s.求木块拉至P点时弹簧的弹性势能;
(2)如果在线的另一端不是施加恒力,而是悬挂一个质量为M的物块,如图乙所示,木块也从初始位置O由静止开始向右运动,求当木块通过P点时的速度大小.

(1)图甲中,在线的另一端施加一竖直向下的大小为F的恒力,木块离开初始位置O由静止开始向右运动,弹簧开始发生伸长形变,已知木块过P点时,速度大小为v,O、P两点间距离为s.求木块拉至P点时弹簧的弹性势能;
(2)如果在线的另一端不是施加恒力,而是悬挂一个质量为M的物块,如图乙所示,木块也从初始位置O由静止开始向右运动,求当木块通过P点时的速度大小.

分析:(1)用力F拉木块至P点,根据功能关系求解
(2)悬挂钩码M时,当木块运动到P点时,弹簧的弹性势能仍为Ep,由机械能守恒定律列出等式求解.
(2)悬挂钩码M时,当木块运动到P点时,弹簧的弹性势能仍为Ep,由机械能守恒定律列出等式求解.
解答:解:(1)用力F拉木块至P点时,设此时弹簧的弹性势能为EP,
根据功能关系有Fs=EP+
mv2…①
代入数据可解得:EP=Fs-
mv2…②
(2)悬挂钩码M时,当木块运动到P点时,弹簧的弹性势能仍为Ep,
设木块的速度为v′,由机械能守恒定律得:
Mgs=EP+
(m+M)v′2…③
联立②③解得v′=
答:(1)木块拉至P点时弹簧的弹性势能是Fs-
mv2;
(2)当木块通过P点时的速度大小是
.
根据功能关系有Fs=EP+
| 1 |
| 2 |
代入数据可解得:EP=Fs-
| 1 |
| 2 |
(2)悬挂钩码M时,当木块运动到P点时,弹簧的弹性势能仍为Ep,
设木块的速度为v′,由机械能守恒定律得:
Mgs=EP+
| 1 |
| 2 |
联立②③解得v′=
|
答:(1)木块拉至P点时弹簧的弹性势能是Fs-
| 1 |
| 2 |
(2)当木块通过P点时的速度大小是
|
点评:正确受力分析,明确各种功能关系,是解答这类问题的关键,这类问题对于提高学生的分析综合能力起着很重要的作用.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目

 (2009?天津模拟)如图甲所示,质量为2m的长木板静止地放在光滑的水平面上,另一质量为m的小铅块(可视为质点)以水平速度v0滑上木板的左端,恰能滑至木板的右端且与木板保持相对静止,铅块在运动过程中所受到的摩擦力始终不变.若将木板分成长度与质量均相等(即m1=m2=m)的两段1、2后,将它们紧挨着放在同一水平面上,让小铅块以相同的初速度v0由木板1的左端开始运动,如图乙所示,则下列说法正确的是( )
(2009?天津模拟)如图甲所示,质量为2m的长木板静止地放在光滑的水平面上,另一质量为m的小铅块(可视为质点)以水平速度v0滑上木板的左端,恰能滑至木板的右端且与木板保持相对静止,铅块在运动过程中所受到的摩擦力始终不变.若将木板分成长度与质量均相等(即m1=m2=m)的两段1、2后,将它们紧挨着放在同一水平面上,让小铅块以相同的初速度v0由木板1的左端开始运动,如图乙所示,则下列说法正确的是( )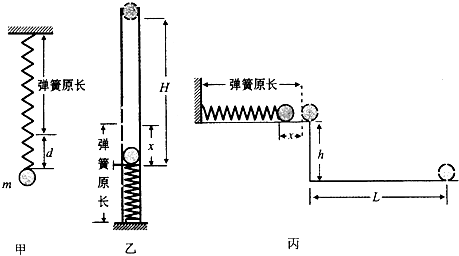 由理论分析可得,弹簧的弹性势能公式为
由理论分析可得,弹簧的弹性势能公式为