题目内容
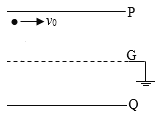
【题目】如图,两金属板P、Q水平放置,间距为d,两金属板正中间有一水平放置的金属网G,P、Q、G的尺寸相同,G接地,P、Q的电势均为φ(φ>0)。质量为m、电荷量为q(q>0)的粒子自P板左下边缘以速度v0平行于纸面水平射入电场,重力忽略不计。
(1)求粒子第一次穿过G时的动能,以及它从射入电场至此时在水平方向上的位移大小;
(2)若粒子恰好从Q板的右上方边缘离开电场,则金属板的长度至少应为多少?
【答案】(1)![]()
![]() (2)
(2)![]()
【解析】
(1)由题意可知PG、QG间场强大小相等,均指向G。则板间电场强度为:
![]()
设粒子第一次到达G时动能为![]() ,则根据动能定理可知:
,则根据动能定理可知:
![]() ,
,
解得:
![]()
粒子在PG间做类平抛运动,有:
![]()
![]()
而加速度有电场力提供有:
![]()
联立以上各式解得:
![]()
(2)由题意可知当粒子恰好从Q板的右上方边缘离开电场,当粒子第一次穿过G就从电场的右侧飞出,此时金属板长度最短;由对称性可知,此时金属棒的长度L至少为:
![]()
答:(1)粒子第一次穿过G时的动能![]() ,它从射入电场至此时在水平方向上的位移大小
,它从射入电场至此时在水平方向上的位移大小![]() ;
;
(2)若粒子恰好从Q板的右上方边缘离开电场,则金属板的长度至少应为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目