题目内容
【题目】如图所示,某同学利用电子秤、轻质材料做成的凹形轨道,研究小球通过凹形轨道的运动,由于小球质量远大于凹形轨道的质量,下面计算中可以忽略凹形轨道的质量,已知凹形轨道最下方为半径为R的圆弧轨道,重力加速度为g,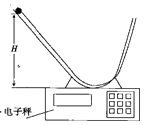
⑴把凹形轨道放在电子秤上,小球放在轨道最低点,电子秤读数为m1 .
⑵让小球从离轨道最低点H处由静止释放,当小球通过轨道最低点时,用手机抓拍出电子秤读数为m2 .
⑶根据电子秤两次读数可知,小球通过轨道最低点时的速度为 , 这说明小球通过凹形轨道最低点时处于填“超重”“失重”或“平衡”)状态.
⑷小球从离轨道最低点高H处由静止释放到通过最低点的过程中克服摩擦力做功为 .
【答案】![]() ;超重;
;超重;![]()
【解析】解:(3)以小球为研究对象,根据牛顿第二定得:
FN﹣m1g=m1 ![]()
据题有:FN=m2g.
联立可得:v= ![]()
小球通过凹形轨道最低点时有向上的加速度,处于超重状态.(4)小球从离轨道最低点高H处由静止释放到通过最低点的过程中,由功能原理知,小球克服摩擦力做功等于小球机械能的减少,为:
Wf=m1gH﹣ ![]() =
= ![]() .
.
故答案为:(3) ![]() ,超重;(4)
,超重;(4) ![]() .
.
(3)小球所受的合外力等于向心力再根据牛顿第三定律可以求出速度,因为小球在轨道最低点是有向上的加速度。根据超重失重判断即可。(4)根据动能定理可以求小球从轨道最低点高H处释放过程中摩擦力所做的功。

练习册系列答案
相关题目