��Ŀ����
����Ŀ����ͼ��һ����ɹ⻬��ֱ�� ![]() Բ��AB���ֲ�ˮƽ��BC���⻬б��CE��ɣ�BC��CE��C���ɼ�С�⻬Բ���������ӣ�б����ˮƽ��ļнǦ�=30�㣬һС����A�����Ϸ���h=0.2m��P���������䣬������A�����߽���������֪С�������m=1kg��Բ���뾶R=0.05m��BC��s=0.1m��С����C���ʱ��t1=0.3s��һ�ε���ͼ�е�D�㣬�־�t2=0.2s�ڶ��ε���D�㣮ȡg=10m/s2 �� ��
Բ��AB���ֲ�ˮƽ��BC���⻬б��CE��ɣ�BC��CE��C���ɼ�С�⻬Բ���������ӣ�б����ˮƽ��ļнǦ�=30�㣬һС����A�����Ϸ���h=0.2m��P���������䣬������A�����߽���������֪С�������m=1kg��Բ���뾶R=0.05m��BC��s=0.1m��С����C���ʱ��t1=0.3s��һ�ε���ͼ�е�D�㣬�־�t2=0.2s�ڶ��ε���D�㣮ȡg=10m/s2 �� ��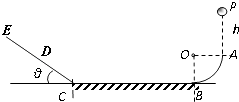
��1��С����һ�ε���Բ�����B���˲�䣬�ܵ��������N�Ĵ�С��
��2��С�����ˮƽ��BC��Ķ�Ħ��������=��
��3��С�������ֹͣ��λ�ã�
���𰸡�
��1��
�⣺�������B��ʱ�ٶȴ�СΪvB��
�ɻ�е���غ㶨�ɵã�mg��h+R��= ![]() mvB2��
mvB2��
��Բ�����B�㣬��ţ�ٵڶ����ɵã�N��mg=m ![]() ��
��
��ã�vB= ![]() m/s��N=110N
m/s��N=110N
��2��
�⣺�������CE�μ��ٶ�Ϊa��
��ţ�ٵڶ����ɵã�a=gsin��=5m/s2��
������һ�ξ���C����ٶ�Ϊvc��
��C���ϻ�����ߵ㣬�辭����ʱ����t��
t=t1+ ![]() t2=0.4s��vc=at=2m/s��
t2=0.4s��vc=at=2m/s��
С����B��C���ɶ��ܶ����ã�
����mgs= ![]() mvC2��
mvC2�� ![]() mvB2������=0.5
mvB2������=0.5
��3��
�⣺��С�����B�㶯��ΪEB��ÿ�ξ���BC����ʧ������Ϊ��E��
���E=��mgs=0.5J��EB= ![]() mvB2=2.5J������������������ʧ��
mvB2=2.5J������������������ʧ��
����EB=5��E������С�������ͣ��C��
����������1�����ӿ�ʼ���䵽B����̣�ֻ��������������е���غ㣬�ɻ�е���غ㶨�ɿ����������B����ٶȣ�Ȼ����ţ�ٵڶ����������������ĵ�������2����ţ�ٵڶ�������������CE�ϵļ��ٶȣ����ٶȹ�ʽ������ﵽC����ٶȣ���B��CӦ�ö��ܶ������������Ħ����������3�����ÿ����BCһ�ο˷�Ħ�������Ĺ���Ȼ��ȷ����������λ�ã�
�����㾫����������Ҫ�������������Ͷ��ܶ������ۺ�Ӧ�õ����֪ʶ�㣬��Ҫ��������������ָ��Բ�ģ��������ļ��ٶȣ�������ֻ�ı����ٶȵķ����ı��ٶȵĴ�С���������Ǹ�������Ч��������.�ڷ�����Բ���˶����ʵ��������ʱ��ǧ������������֮��������һ����������Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݲ�����ȷ�����⣮

 Ʒѧ˫�ž�ϵ�д�
Ʒѧ˫�ž�ϵ�д� Сѧ��ĩ���100��ϵ�д�
Сѧ��ĩ���100��ϵ�д� ��ĩ��ϰ���ϵ�д�
��ĩ��ϰ���ϵ�д� ����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
����ѧ�䵥Ԫ������ĩר����100��ϵ�д�