题目内容
1.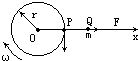 如图所示,质点P以O为圆心在水平面内做匀速圆周运动,半径为r,角速度为ω,当质点P正通过x轴时,另一质量为m的质点由静止开始在水平恒力F的作用下,沿x轴正方向运动,若要使P、Q两质点能在某时刻的速度相同(大小和方向),则力F的可能取值为?
如图所示,质点P以O为圆心在水平面内做匀速圆周运动,半径为r,角速度为ω,当质点P正通过x轴时,另一质量为m的质点由静止开始在水平恒力F的作用下,沿x轴正方向运动,若要使P、Q两质点能在某时刻的速度相同(大小和方向),则力F的可能取值为?
分析 质点Q在沿OA方向从静止开始在光滑水平面上作匀加速直线运动,速度方向水平向右.当质点P运动到圆周的正上方位置时,速度与Q的速度相同,判断经过的时间与周期的关系.经过时间t,根据动量定理列式求解.
解答 解:质点Q在沿OA方向从静止开始在光滑水平面上作匀加速直线运动,速度方向水平向右,故当质点P运动到圆周的正上方位置时,速度与Q的速度相同;
速度v=ωR;
时间t=(n+0.75)T,其中n=0、1、2、…;
对质点Q运用动量定理,有:
Ft=mv;
联立解得:F=$\frac{mv}{t}=\frac{mωR}{(n+0.75)T}$,其中n=0、1、2、…;
答:F的大小应满足条件为:F=$\frac{mωR}{(n+0.75)T}$,其中n=0、1、2、…
点评 该题将匀速圆周运动与匀加速直线运动向结合的题目,解题的关键要考虑圆周运动的多解性,同时注意速度相同的是指速度大小和方向都相同.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
10. 如图所示,公路路面的倾斜角为θ,在弯道路段的半径为R,重力加速度为g.要保证安全,汽车在弯道路段的行驶速度应满足( )
如图所示,公路路面的倾斜角为θ,在弯道路段的半径为R,重力加速度为g.要保证安全,汽车在弯道路段的行驶速度应满足( )
 如图所示,公路路面的倾斜角为θ,在弯道路段的半径为R,重力加速度为g.要保证安全,汽车在弯道路段的行驶速度应满足( )
如图所示,公路路面的倾斜角为θ,在弯道路段的半径为R,重力加速度为g.要保证安全,汽车在弯道路段的行驶速度应满足( )| A. | v=gRtanθ | B. | v=gR2tanθ | C. | v≤$\sqrt{gRsinθ}$ | D. | v≤$\sqrt{gRtanθ}$ |
9.欲使处于基态的氢原子激发,下列措施可行的是( )
| A. | 用10.2eV的光子照射 | B. | 用11eV的光子照射 | ||
| C. | 用14eV的光子照射 | D. | 用11eV的电子碰撞 |
11.如图电路中,P、Q两灯相同,L的电阻不计,则( )
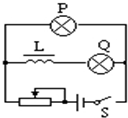

| A. | S断开瞬间,P立即熄灭,Q过一会才熄灭 | |
| B. | S接通瞬间,P、Q同时达正常发光 | |
| C. | S断开瞬间,通过P的电流从右向左 | |
| D. | S断开瞬间,通过Q的电流与原来方向相反 |
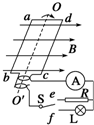 如图所示,矩形线框匝数N=250匝,ab=12cm,ad=10cm,线框置于B=$\frac{2}{π}$T的匀强磁场中,绕垂直于磁场的轴OO′以n=120r/min的转速匀速转动,线框通过滑环与外电路相连,外电路接有R=12Ω的电阻及一只发光电压和熄灭电压都为12V的氖泡L.(线框电阻不计)求:
如图所示,矩形线框匝数N=250匝,ab=12cm,ad=10cm,线框置于B=$\frac{2}{π}$T的匀强磁场中,绕垂直于磁场的轴OO′以n=120r/min的转速匀速转动,线框通过滑环与外电路相连,外电路接有R=12Ω的电阻及一只发光电压和熄灭电压都为12V的氖泡L.(线框电阻不计)求: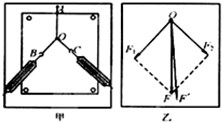 在做“验证力的平行四边形定则”的实验时,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳,图乙是在白纸上根据实验数据画出的图.
在做“验证力的平行四边形定则”的实验时,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳,图乙是在白纸上根据实验数据画出的图.