题目内容
20. 如图所示,带异种电荷的粒子a、b以相同的动能同时从O点射入宽度为d的有界匀强磁场,两粒子的入射方向与磁场边界的夹角分别为30°和60°,且同时到达与O点在同一水平面的P点.则a、b两粒子的质量之比和电量之比分别为( )
如图所示,带异种电荷的粒子a、b以相同的动能同时从O点射入宽度为d的有界匀强磁场,两粒子的入射方向与磁场边界的夹角分别为30°和60°,且同时到达与O点在同一水平面的P点.则a、b两粒子的质量之比和电量之比分别为( )| A. | 3:4 | B. | 4:3 | C. | 2:3 | D. | 3:2 |
分析 粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,作出粒子运动轨迹,求出粒子轨道半径,然后应用牛顿第二定律与粒子做圆周运动的周期公式分析答题
解答 解:粒子运动轨迹如图所示:
由几何知识得,粒子a的半径:r1=$\frac{\frac{d}{2}}{sin60°}$=$\frac{\sqrt{3}}{3}$,
粒子b的半径为:r2=$\frac{\frac{d}{2}}{sin30°}$=d,
粒子在磁场中做圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:
qvB=m$\frac{{v}^{2}}{r}$,解得:r=$\frac{mv}{qB}$,则:r1=$\frac{{m}_{1}{v}_{1}}{{q}_{1}B}$=$\frac{\sqrt{2{m}_{1}{E}_{K}}}{{q}_{1}B}$,r2=$\frac{{m}_{2}{v}_{2}}{{q}_{2}B}$=$\frac{\sqrt{2{m}_{2}{E}_{K}}}{{q}_{2}B}$,
解得:$\frac{\sqrt{{m}_{1}}}{{q}_{1}}$:$\frac{\sqrt{{m}_{2}}}{{q}_{2}}$=r1:r2=1:$\sqrt{3}$ ①,
粒子在磁场中做圆周运动的周期:T=$\frac{2πm}{qB}$,
粒子在磁场中的运动时间:t=$\frac{θ}{2π}$T=$\frac{θm}{qB}$,
粒子a运动时间:t1=$\frac{{θ}_{1}{m}_{1}}{{q}_{1}B}$=$\frac{2π{m}_{1}}{3{q}_{1}B}$,
粒子b的运动时间:t2=$\frac{{θ}_{2}{m}_{2}}{{q}_{2}B}$=$\frac{π{m}_{2}}{3{q}_{2}B}$,
与题意可知,两个粒子的运动时间相同,即:t1=t2,$\frac{2π{m}_{1}}{3{q}_{1}B}$=$\frac{π{m}_{2}}{3{q}_{2}B}$,
整理得:$\frac{{m}_{1}}{{q}_{1}}$:$\frac{{m}_{2}}{{q}_{2}}$=1:2 ②
由①②解得:q1:q2=3:2,m1:m2=3:4,故AD正确;
故选:AD.
点评 本题考查了粒子在磁场中的运动,求解有关带电粒子在有界磁场中的运动问题的关键是画出轨迹图,并根据几何知识确定圆心求出半径和圆心角,再结合圆周运动的有关规律联立即可求解.

| A. | 9.3m/s | B. | 12.5 m/s | C. | 12.4 m/s | D. | 10 m/s |
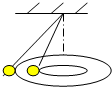
| A. | 运动的周期相同 | B. | 受到的拉力一定相同 | ||
| C. | 运动的角速度相同 | D. | 向心加速度相同 |
| A. | 由E=$\frac{F}{q}$可知,某电场的场强E与q成反比,与F成正比 | |
| B. | 正、负试探电荷在电场中同一点受到的电场力方向相反,所以某一点场强方向与放入试探电荷的正负有关 | |
| C. | 电场中某一点的场强与放入该点的试探电荷的正负无关 | |
| D. | 从点电荷场强计算式分析库仑定律的表达式F=k$\frac{{q}_{1}{q}_{2}}{{r}^{2}}$,式$\frac{k{q}_{2}}{{r}^{2}}$是点电荷q2产生的电场在点电荷q1处的场强大小,而$\frac{k{q}_{1}}{{r}^{2}}$是点电荷q1产生的电场在q2处场强的大小 |
 污水处理站的管道中安装了如图所示的流量计,该装置由绝缘材料制成,长、宽、高分别为a、b、c.左右两端开口,在垂直于上下底面方向加磁感应强度为B的匀强磁场,在前后两个面的内侧固定有金属板作为电极,当含有大量正负离子(其重力不计)的污水充满管口从左向右流经该装置时,测出电极间的电势差U,就可测出污水流量Q(单位时间内流出的污水体积).则( )
污水处理站的管道中安装了如图所示的流量计,该装置由绝缘材料制成,长、宽、高分别为a、b、c.左右两端开口,在垂直于上下底面方向加磁感应强度为B的匀强磁场,在前后两个面的内侧固定有金属板作为电极,当含有大量正负离子(其重力不计)的污水充满管口从左向右流经该装置时,测出电极间的电势差U,就可测出污水流量Q(单位时间内流出的污水体积).则( )| A. | 前表面的电势低于后表面的电势 | |
| B. | 若污水为电中性,则两极间的电势差为零 | |
| C. | 若污水中离子浓度越高,则两极间的电势差越大 | |
| D. | 若管道中污水流量越大,则两极间的电势差越大 |
| A. | 加速度 | B. | 位移 | C. | 回复力 | D. | 动能 |

| A. | 灯泡L开路 | B. | 电阻R1、R2中有开路发生 | ||
| C. | 电阻R1、R2中有短路发生 | D. | 灯泡L和电阻R1都发生了开路 |
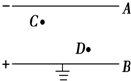 如图所示,平行金属带电极板A、B间可看作匀强电场,场强E=1.2×103V/m,极板间距离d=5cm,电场中C和D分别到A、B两板的距离均为1cm,B极板接地,求:
如图所示,平行金属带电极板A、B间可看作匀强电场,场强E=1.2×103V/m,极板间距离d=5cm,电场中C和D分别到A、B两板的距离均为1cm,B极板接地,求: