题目内容
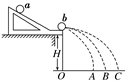
彭仁合作学习小组共同探究家中水龙头的滴水情况。当水龙头拧得较小时,可以控制水一滴一滴地滴落到地面上,小组发现:第一滴水碰地的同时,第二滴水刚好从水龙头处下落。为了测算水滴下落的平均速度,同学们找来了秒表和卷尺。首先量出水龙头口离地面的高度h,再用秒表计时。当他们听到某一水滴滴在地上声音的同时,开启秒表开始计时,并数“1”,以后每听到一声水滴声,依次数“2、3……”,一直数到“n”时,按下秒表停止计时,读出秒表的示数为t。
(1)水滴在空中运动的平均速度的表达式为 ;
(2)测得h=1m,当数到n=20时秒表的示数 t=8.7s,则水滴下落的平均速度为 m/s;
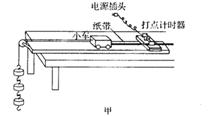
(3)为了进一步探究水滴下落的平均速度和下落高度的关系,大家又做了以下实验:找来一块挡板,让水滴落在挡板上。改变挡板和水龙头口之间的距离h,并仔细调节水龙头滴水的快慢,使得总是在前一滴水滴到挡板上的同时,后一滴水刚好开始下落。计时方法仍和上面一样。从实验中又获得了如下表所示的6组数据(连同上面的一组共有7组数据)。请选取合适的坐标轴,标上数据和单位,作出相应的图象,并根据图象写出平均速度和下落高度的函数关系为 。
(1)水滴在空中运动的平均速度的表达式为 ;
(2)测得h=1m,当数到n=20时秒表的示数 t=8.7s,则水滴下落的平均速度为 m/s;
(3)为了进一步探究水滴下落的平均速度和下落高度的关系,大家又做了以下实验:找来一块挡板,让水滴落在挡板上。改变挡板和水龙头口之间的距离h,并仔细调节水龙头滴水的快慢,使得总是在前一滴水滴到挡板上的同时,后一滴水刚好开始下落。计时方法仍和上面一样。从实验中又获得了如下表所示的6组数据(连同上面的一组共有7组数据)。请选取合适的坐标轴,标上数据和单位,作出相应的图象,并根据图象写出平均速度和下落高度的函数关系为 。

| 次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 高度 h(m) | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.8 |
| 平均速度 v(m/s) | 0.97 | 1.19 | 1.38 | 1.5 4 | 1.6 8 | 1.9 5 |
(1)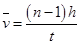
(2)平均速度v≈2.18m/s
(3)图线如下图
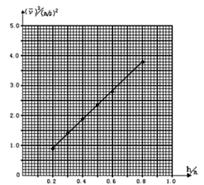
平均速度和下落高度的函数关系为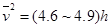
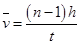
(2)平均速度v≈2.18m/s
(3)图线如下图

平均速度和下落高度的函数关系为
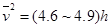
试题分析:(1)水滴在空中运动时间
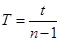 ,所以
,所以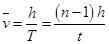
(2)将h=1m、n=20、t=8.7s代入平均速度
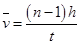 得v≈2.18m/s
得v≈2.18m/s(3)求出速度的平方如下表
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 高度 h(m) | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.8 |
| 平均速度 v(m/s) | 0.97 | 1.19 | 1.38 | 1.54 | 1.68 | 1.95 |
平均速度平方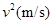 | 0.94 | 1.42 | 1.90 | 2.37 | 2.82 | 3.80 |
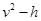 图象如下,
图象如下,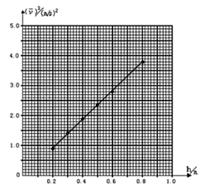
由图线可得可得出平均速度和下落高度的函数关系为
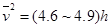
点评:本题找平均速度和下落高度的函数关可以用图像法,一般只有直线才能得出准却函数关系,所以要多假设几种函数关系,画出图像,选取合适的找出函数关系。

练习册系列答案
相关题目
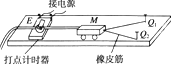


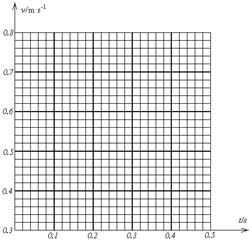

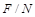
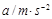
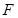 或
或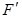 )
)