题目内容
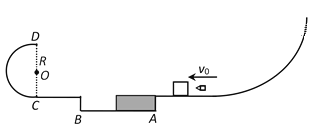
【题目】如图所示,水平面上AB间有一长度x=4m的凹槽,长度为L=2m、质量M=1kg的木板静止于凹槽右侧,木板厚度与凹槽深度相同,水平面左侧有一半径R=0.4m的竖直半圆轨道,右侧有一个足够长的圆弧轨道,A点右侧静止一质量m1=0.98kg的小木块.射钉枪以速度v0=100m/s射出一颗质量m0=0.02kg的铁钉,铁钉嵌在木块中并滑上木板,木板与木块间动摩擦因数μ=0.05,其它摩擦不计.若木板每次与A、B相碰后速度立即减为0,且与A、B不粘连,重力加速度g=10m/s2.求:
(1)铁钉射入木块后共同的速度V;
(2)木块经过竖直圆轨道最低点C时,对轨道的压力大小FN;
(3)木块最终停止时离A点的距离s.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】(1) 设铁钉与木块的共同速度为v,取向左为正方向,根据动量守恒定律得:
![]()
解得:![]() ;
;
(2) 木块滑上薄板后,木块的加速度![]() ,且方向向右
,且方向向右
板产生的加速度![]() ,且方向向左
,且方向向左
设经过时间t,木块与木板共同速度![]() 运动
运动
则:![]()
此时木块与木板一起运动的距离等于木板的长度
![]()
故共速时,恰好在最左侧B点,此时木块的速度![]()
木块过C点时对其产生的支持力与重力的合力提供向心力,则:
![]()
代入相关数据解得:FN=12.5N.
由牛顿第三定律知,木块过圆弧C点时对C点压力为12.5N;
(3) 木块还能上升的高度为h,由机械能守恒有:![]()
![]()
木块不脱离圆弧轨道,返回时以1m/s的速度再由B处滑上木板,设经过t1共速,此时木板的加速度方向向右,大小仍为a2,木块的加速度仍为a1,
则:![]() ,解得:
,解得:![]()
此时![]()
![]()
碰撞后,v薄板=0,木块以速度v3=0.5m/s的速度向右做减速运动
设经过t2时间速度为0,则![]()
![]()
故ΔL=L﹣△x'﹣x=1.25m
即木块停止运动时离A点1.25m远。

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目