题目内容
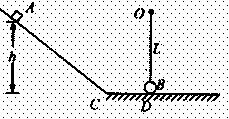
如图所示，光滑斜面与水平地面在C点平滑连接，质量为0．4kg的滑块A无初速地沿斜面滑下后，又沿水平地面运动至D与质量为0.8kg的小球B发生正碰，碰撞时没有能量损失．B球用长为L=O.32m的细线悬于O点，其下端恰与水平地面上的D点相切． 已知滑块A与水平地面间的动摩擦因数
＝0.1，C、D间距离LCD＝1．4m，碰撞后B球恰好能在竖直面做作完整的圆周运动，g取10m/s2,.求：
(1)滑块A在斜面上滑下时的高度h；(2)滑块A最终与D点间的距离．
(1) 1.94m (2) 
解析:
（1）设小滑块A滑至D点与小球B碰撞前的速度为
，碰后A、B的速度分别为
，则小滑块滑动至D过程中，
2分
在D点A、B发生碰撞，动量守恒， 
2分
机械能守恒， 
1分
小球B刚好作完整的圆周运动，设到达最高点时的速度为
，则在最高点时，
2分
从最低点到最高点过程中，
1分
由①-⑤可得h=1.94m ,
=-2m/s (负号表示碰后滑块A速度向左) 2分
（2）设碰后小滑块A在水平面上滑动的路程为S，则有
2分
解得
1分
因为
,所以滑块先自左滑过C点后，又从斜面返回并静止在C、D之间
的一点上 3分
故小滑块最终与D点间的距离为 2分
练习册系列答案
相关题目
如图所示，光滑斜面与水平面在B点平滑连接，质量为0.20kg的物体从斜面上的A点由静止开始下滑，经过B点后进入水平面（设经过B点前后速度大小不变），最后停在水平面上的C点．每隔0.20s通过速度传感器测量物体的瞬时速度，下表给出了部分测量数据．取g=10m/s2．
如图所示，光滑斜面与水平面在B点平滑连接，质量为0.20kg的物体从斜面上的A点由静止开始下滑，经过B点后进入水平面（设经过B点前后速度大小不变），最后停在水平面上的C点．每隔0.20s通过速度传感器测量物体的瞬时速度，下表给出了部分测量数据．取g=10m/s2．
如图所示，光滑斜面与水平地面在C点平滑连接，质量为0.4kg的滑块A无初速地沿斜面滑下后，又沿水平地面运动至D与质量为0.8kg的小球B发生正碰，碰撞时没有能量损失．B球用长为L=O．32m的细线悬于O点，其下端恰与水平地面土的D点相切． 已知滑块A与水平地面间的动摩擦因数μ=0.1，C、D间距离LCD=1.4m，碰撞后B球恰好能在竖直面做作完整的圆周运动，g取10m/s2．求：
如图所示，光滑斜面与水平成θ角，在斜面上放一个质量为m的圆球，再用光滑的挡板住，现在缓慢地改变挡板A与斜面的夹角α，当α=
如图所示，光滑斜面与水平地面在C点平滑连接，质量为0.4kg的滑块A无初速地沿斜面滑下后，又沿水平地面运动至D点与质量也为0.4kg 的小球B发生正碰，碰撞时没有机械能损失，小球B用长为L=0.32m的细绳悬于O点，其下端恰好与水平地面上的D点相切，已知滑块与水平地面间的动摩擦因素为μ=0.1，C、D间距LCD=1.4m，碰后B球恰好能在竖直平面内做完整的圆周运动，g=l0m/s2，求：