题目内容
如图所示，光滑斜面与水平成θ角，在斜面上放一个质量为m的圆球，再用光滑的挡板住，现在缓慢地改变挡板A与斜面的夹角α，当α=90
90
°时，A板对球的弹力最小，其最小值为mgsinθ
mgsinθ
．分析：本题是应用平衡条件对受力进行动态分析，找出不变的力：重力，斜面支持力的方向，挡板和斜面对小球支持力的合力；根据不变的力来判断变化的力是如何变化的．
解答：解：对物体受力分析如图：
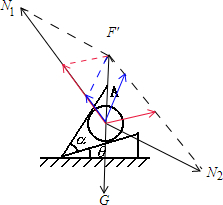
挡板和斜面对小球支持力的合力F′保持不变，斜面对小球的支持力方向不变，当挡板转动时，挡板对小球的弹力先变小后变大，所以最小时如图绿颜色所示：
此时这个最小的弹力与N1方向垂直，即此时α=90°
在直角三角形中：由三角函数关系得：sinθ=
=
解得：N2=mgsinθ
故答案为：α=90°时，A板对球的弹力最小，其最小值为 mgsinθ．
挡板和斜面对小球支持力的合力F′保持不变，斜面对小球的支持力方向不变，当挡板转动时，挡板对小球的弹力先变小后变大，所以最小时如图绿颜色所示：
此时这个最小的弹力与N1方向垂直，即此时α=90°
在直角三角形中：由三角函数关系得：sinθ=
| N2 |
| F′ |
| N2 |
| mg |
解得：N2=mgsinθ
故答案为：α=90°时，A板对球的弹力最小，其最小值为 mgsinθ．
点评：此题考查受力平衡的一个重要应用：动态分析．动态分析时就是先找不变的物理量，由不变来判断变化的力是如何变化的．
练习册系列答案
相关题目
如图所示，光滑斜面与水平面在B点平滑连接，质量为0.20kg的物体从斜面上的A点由静止开始下滑，经过B点后进入水平面（设经过B点前后速度大小不变），最后停在水平面上的C点．每隔0.20s通过速度传感器测量物体的瞬时速度，下表给出了部分测量数据．取g=10m/s2．
如图所示，光滑斜面与水平面在B点平滑连接，质量为0.20kg的物体从斜面上的A点由静止开始下滑，经过B点后进入水平面（设经过B点前后速度大小不变），最后停在水平面上的C点．每隔0.20s通过速度传感器测量物体的瞬时速度，下表给出了部分测量数据．取g=10m/s2．
如图所示，光滑斜面与水平地面在C点平滑连接，质量为0.4kg的滑块A无初速地沿斜面滑下后，又沿水平地面运动至D与质量为0.8kg的小球B发生正碰，碰撞时没有能量损失．B球用长为L=O．32m的细线悬于O点，其下端恰与水平地面土的D点相切． 已知滑块A与水平地面间的动摩擦因数μ=0.1，C、D间距离LCD=1.4m，碰撞后B球恰好能在竖直面做作完整的圆周运动，g取10m/s2．求：
如图所示，光滑斜面与水平地面在C点平滑连接，质量为0.4kg的滑块A无初速地沿斜面滑下后，又沿水平地面运动至D点与质量也为0.4kg 的小球B发生正碰，碰撞时没有机械能损失，小球B用长为L=0.32m的细绳悬于O点，其下端恰好与水平地面上的D点相切，已知滑块与水平地面间的动摩擦因素为μ=0.1，C、D间距LCD=1.4m，碰后B球恰好能在竖直平面内做完整的圆周运动，g=l0m/s2，求：