题目内容
竖直平面内，一带正电的小球，系于长为L不可伸长的轻线一端，线的另一端固定为0点，它们处在匀强电场中，电场的方向水平向右，场强的大小为E．已知电场对小球的作用力的大小等于小球的重力．现先把小球拉到图中的P1处，使轻线伸直，并与场强方向平行，然后由静止释放小球，已知小球在经过最低点的瞬间，因受线的拉力作用，其竖直方向上的速度突变为零，水平方向分量没有变化，则小球到达与P1点等高的P2时线上张力为（ ）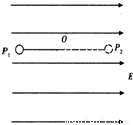
A．mg
B．2mg
C．3mg
D．4mg
【答案】分析：小球在电场力和重力的作用下做加速运动，当绳被拉直的时候，沿着绳的速度的大小变为零，之后球在重力和电场力的作用下继续向右运动，从绳被拉直到到达P2的过程中，根据动能定理可以求得到达P2时速度的大小．根据径向的合力提供向心力求出绳子的张力大小．
解答：解：小球由静止释放到最低点的过程中受到电场力和重力两个力，其合力的方向是由P1指向最低点，因此小球做匀加速直线运动，
水平分量是vx=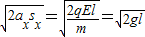
．
在到达P2的过程中，由动能定理有
Eql-mgl=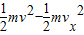
即v=vx=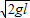
．
根据牛顿第二定律得，T-qE=m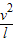
解得T=3mg．故C正确，A、B、D错误．
故选C．
点评：在小球运动的全过程中是不能应用动能定理来计算的，因为在绳被拉直的时候，球的动能有损失，这是本题常出错的地方．
解答：解：小球由静止释放到最低点的过程中受到电场力和重力两个力，其合力的方向是由P1指向最低点，因此小球做匀加速直线运动，
水平分量是vx=
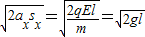．在到达P2的过程中，由动能定理有
Eql-mgl=
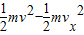
即v=vx=
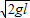．根据牛顿第二定律得，T-qE=m
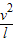
解得T=3mg．故C正确，A、B、D错误．
故选C．
点评：在小球运动的全过程中是不能应用动能定理来计算的，因为在绳被拉直的时候，球的动能有损失，这是本题常出错的地方．
练习册系列答案
阅读快车系列答案
相关题目
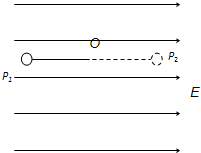（2009?湖南模拟）竖直平面内，一带正电的小球，系于长为L不可伸长的轻线一端，线的另一端固定为0点，它们处在匀强电场中，电场的方向水平向右，场强的大小为E．已知电场对小球的作用力的大小等于小球的重力．现先把小球拉到图中的P1处，使轻线伸直，并与场强方向平行，然后由静止释放小球，已知小球在经过最低点的瞬间，因受线的拉力作用，其竖直方向上的速度突变为零，水平方向分量没有变化，则小球到达与P1点等高的P2时线上张力为（ ）
如图所示，竖直平面内，一带正电的小球，系于长为L的不可伸长的轻线一端，线的另一端固定于O点，它们处在匀强电场中，电场的方向水平向右，场强的大小为E．已知电场对小球的作用力的大小等于小球的重力．现先把小球拉到图中的P1处，使轻线伸直，并与场强方向平行，然后由静止释放小球．已知小球在经过最低点的瞬间，因受线的拉力作用，其速度的竖直分量突变为零，水平分量没有变化，（不计空气阻力）则小球到达与P1点等高的P2点时线上张力T是多少．
