题目内容
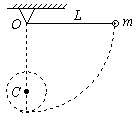
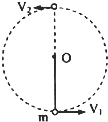 长为L的轻绳的一端固定在O点,另一端栓一个质量为m的小球.使小球以O为圆心,L为半径在竖直平面内做圆周运动,(如图所示.重力加速度g.)已知小球在t1时刻通过最高点时受到轻绳的拉力为mg.经多次圆周运动后在t2时刻通过最低点时受到轻绳的拉力为6mg则
长为L的轻绳的一端固定在O点,另一端栓一个质量为m的小球.使小球以O为圆心,L为半径在竖直平面内做圆周运动,(如图所示.重力加速度g.)已知小球在t1时刻通过最高点时受到轻绳的拉力为mg.经多次圆周运动后在t2时刻通过最低点时受到轻绳的拉力为6mg则(1)小球在t1时刻通过最高点时速度为多大?
(2)小球在t2时刻通过最低点时速度为多大?
(3)求小球从t1时刻到t2时刻的过程中克服空气阻力做的功.
分析:小球在竖直平面内做圆周运动,在最高点和最低点,合外力提供向心力.根据向心力公式求出小球在最高点和最低点的速度.根根据动能定理求出小球从t1时刻到t2时刻的过程中克服空气阻力做的功
解答:解:(1)在最高点,根据向心力公式得:m
=mg+mg
解得:v1=
(2)在最低点,根据向心力公式得:m
=6mg-mg=5mg
解得:v2=
(3)小球从t1时刻到t2时刻的过程中运用动能定理得:
W+2mgL=
mv22-
mv12
解得W=-
mg
即 W克=
mgL
答:(1)小球在t1时刻通过最高点时速度为
;
(2)小球在t2时刻通过最低点时速度为
;
(3)小球从t1时刻到t2时刻的过程中克服空气阻力做的功为
mgL.
| v12 |
| L |
解得:v1=
| 2gL |
(2)在最低点,根据向心力公式得:m
| v22 |
| L |
解得:v2=
| 5gL |
(3)小球从t1时刻到t2时刻的过程中运用动能定理得:
W+2mgL=
| 1 |
| 2 |
| 1 |
| 2 |
解得W=-
| 1 |
| 2 |
即 W克=
| 1 |
| 2 |
答:(1)小球在t1时刻通过最高点时速度为
| 2gL |
(2)小球在t2时刻通过最低点时速度为
| 5gL |
(3)小球从t1时刻到t2时刻的过程中克服空气阻力做的功为
| 1 |
| 2 |
点评:本题主要考查了向心力公式及机械能守恒定律的直接应用,知道竖直平面内做圆周运动,在最高点和最低点,合外力提供向心力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
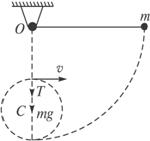
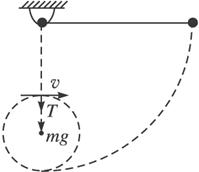
 ,如图所示。欲使小球到达最低点后以C为圆心至少做一次完整的圆周运动,则h应满足什么条件?
,如图所示。欲使小球到达最低点后以C为圆心至少做一次完整的圆周运动,则h应满足什么条件?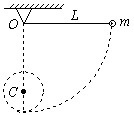
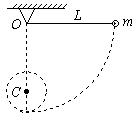 圆心至少做一次完整的圆周运动,则h应满足什么条件?
圆心至少做一次完整的圆周运动,则h应满足什么条件?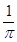 ,如图所示,(1) 欲使小球到达最低点后以C为圆心至少做一次完整的圆周运动,则h应满足什么条件?
,如图所示,(1) 欲使小球到达最低点后以C为圆心至少做一次完整的圆周运动,则h应满足什么条件?