题目内容
14.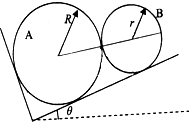 如图所示,在斜面上放置两个光滑球A和B,两球的质量均为m=1.2kg,它们的半径分别是R和r,球A左侧有一垂直于斜面的挡板,两球放置于斜面上均处于静止状态.若斜面与水平间的夹角为θ=30°,重力加速度为g=10m/s2.(sin37°=0.6,cos37°=0.8)
如图所示,在斜面上放置两个光滑球A和B,两球的质量均为m=1.2kg,它们的半径分别是R和r,球A左侧有一垂直于斜面的挡板,两球放置于斜面上均处于静止状态.若斜面与水平间的夹角为θ=30°,重力加速度为g=10m/s2.(sin37°=0.6,cos37°=0.8)(1)在图中画出B球受的力;
(2)若B球质量不变,但半径可以变化,为使两球间的弹力最小,R和r的比值是多少?
(3)求A、B两球之间的最小弹力?
分析 本题先对B球研究,分析受力,运用作图法,由平衡条件分析;
由图确定出A对B的弹力最小时两球间的弹力的方向,根据几何关系分析求解;
解答 解:(1)以B球为研究对象,分析受力情况:重力mg、斜面的支持力N和A对B的弹力F,

(2)如图,作出F在三个不同角度时力的合成图,由图看出,
斜面倾角θ一定,由图根据几何知识得知,当N与F垂直时F最小,即两球间的弹力最小,
此时,R=r时,即R和r的比值是1.
(3)根据三角函数关系得
A、B两球之间的最小弹力F=mgsin30°=6N
答:(1)如图;
(2)为使两球间的弹力最小,R和r的比值是1;
(3)A、B两球之间的最小弹力是6N.
点评 本题一要灵活选择研究对象,二要灵活选择研究方法,本题采用图解法和函数法相结合研究,比较简便.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6. 如图所示,小物块A与水平圆盘之间保持相对静止.若小物块A跟随圆盘做匀速圆周运动,则A受到的力有( )
如图所示,小物块A与水平圆盘之间保持相对静止.若小物块A跟随圆盘做匀速圆周运动,则A受到的力有( )
 如图所示,小物块A与水平圆盘之间保持相对静止.若小物块A跟随圆盘做匀速圆周运动,则A受到的力有( )
如图所示,小物块A与水平圆盘之间保持相对静止.若小物块A跟随圆盘做匀速圆周运动,则A受到的力有( )| A. | 重力、支持力、沿切线的摩擦力 | B. | 重力、支持力、向心力、摩擦力 | ||
| C. | 重力、支持力、指向圆心的摩擦力 | D. | 重力、支持力 |
7.关于光电效应,下列说法正确的是( )
| A. | 光电子的最大初动能与入射光的频率成正比 | |
| B. | 用不可见光照射金属一定比用可见光照射同种金属产生的光电子的初动能大 | |
| C. | 对同种金属只要入射光强度足够大,就会发生光电效应 | |
| D. | 光电效应的发生几乎不需要时间积累,只要入射光的波长小于金属的极限波长即可 |
2.人和气球离地高度为h,恰好悬浮在空中,气球质量为M,人的质量为m,人要从气球下拴着的软绳上安全的下滑到地面,软绳的长度至少为多少?( )
| A. | $\frac{Mh}{M+m}$ | B. | $\frac{mh}{M+m}$ | C. | $\frac{(m+M)h}{M}$ | D. | $\frac{(m+M)h}{m}$ |
19.一列简谐横波沿直线由A向B传播,A、B两质点的平衡位置相距3m,t1=0时,质点A处于波峰位置,质点B刚好在平衡位置且向y轴负方向运动;t2=0.5s时,质点B恰在波谷,则下列关于这列波的说法正确的是( )
| A. | 波长可能是12m | B. | 波长一定是4m | C. | 周期一定是2s | D. | 波速可能是10m/s |
3.质量为m的物体,由静止开始竖直下落,由于阻力作用,下落的加速度为$\frac{1}{4}$g,在物体下落h的过程中,下列说法中正确的是( )
| A. | 物体克服阻力所做的功为$\frac{1}{4}$mgh | B. | 物体的重力势能减少了mgh | ||
| C. | 物体的动能增加了$\frac{3}{4}$mgh | D. | 物体的机械能减少了$\frac{1}{4}$mgh |
4. 一个半径为R的$\frac{1}{4}$光滑圆弧与一倾角为30°的光滑斜面通过一小段光滑圆弧相接于O点,如图所示,斜面高也为R,一质点第一次从圆弧的A点由静止下滑,第二次从圆弧上的C点由静止下滑(∠CO1O=60°),则( )
一个半径为R的$\frac{1}{4}$光滑圆弧与一倾角为30°的光滑斜面通过一小段光滑圆弧相接于O点,如图所示,斜面高也为R,一质点第一次从圆弧的A点由静止下滑,第二次从圆弧上的C点由静止下滑(∠CO1O=60°),则( )
 一个半径为R的$\frac{1}{4}$光滑圆弧与一倾角为30°的光滑斜面通过一小段光滑圆弧相接于O点,如图所示,斜面高也为R,一质点第一次从圆弧的A点由静止下滑,第二次从圆弧上的C点由静止下滑(∠CO1O=60°),则( )
一个半径为R的$\frac{1}{4}$光滑圆弧与一倾角为30°的光滑斜面通过一小段光滑圆弧相接于O点,如图所示,斜面高也为R,一质点第一次从圆弧的A点由静止下滑,第二次从圆弧上的C点由静止下滑(∠CO1O=60°),则( )| A. | 质点两次离开O点后均做平抛运动而落在水平面上 | |
| B. | 质点两次离开O点后均做平抛运动,但均落在斜面上 | |
| C. | 质点两次离开O点前瞬间对轨道压力的比为3:2 | |
| D. | 质点第一次离开O点后做平抛运动,第二次沿斜面下滑 |
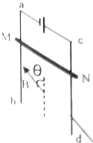
 如图所示,电阻为R的金属棒MN水平靠在光滑的竖直导轨外侧,与导轨接触良好,导轨的上端与电源连接,导轨电阻不计,整个装置置于方向与导轨平面成θ角且与金属棒MN垂直的匀强磁场中,图中所加磁场的方向能使MN静止的是( )
如图所示,电阻为R的金属棒MN水平靠在光滑的竖直导轨外侧,与导轨接触良好,导轨的上端与电源连接,导轨电阻不计,整个装置置于方向与导轨平面成θ角且与金属棒MN垂直的匀强磁场中,图中所加磁场的方向能使MN静止的是( )


 如图所示,在水平桌面上放有长木板C,C上右端是固定挡板P,在C上左端和中点处各放有小物块A和B,A、B的尺寸以及P的厚度皆可忽略不计,A、B之间和B、P之间的距离皆为L.设木板C与桌面之间无摩擦,A、C之间和B、C之间的静摩擦因数及滑动摩擦因数均为μ;最大静摩擦力等于滑动摩擦力大小,A、B、C(连同挡板P)的质量都为m,开始时,B和C静止,A以某一初速度v0向右运动,重力加速度为g.求:
如图所示,在水平桌面上放有长木板C,C上右端是固定挡板P,在C上左端和中点处各放有小物块A和B,A、B的尺寸以及P的厚度皆可忽略不计,A、B之间和B、P之间的距离皆为L.设木板C与桌面之间无摩擦,A、C之间和B、C之间的静摩擦因数及滑动摩擦因数均为μ;最大静摩擦力等于滑动摩擦力大小,A、B、C(连同挡板P)的质量都为m,开始时,B和C静止,A以某一初速度v0向右运动,重力加速度为g.求: