题目内容
15.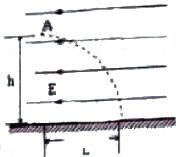 如图所示,地面上放有水平向左的匀强电场,一质量为m,电荷量为q的小球以一定水平初速度从A处抛出,落地时的速度方向恰好沿竖直方向,已知A处距地面的高度为h,小球的水平位移为L,重力加速度为g,求
如图所示,地面上放有水平向左的匀强电场,一质量为m,电荷量为q的小球以一定水平初速度从A处抛出,落地时的速度方向恰好沿竖直方向,已知A处距地面的高度为h,小球的水平位移为L,重力加速度为g,求(1)电场强度E的大小和水平初速度V0的大小;
(2)小球运动到距地面的高度为$\frac{h}{2}$时的动能.
分析 (1)小球在电场中做类平抛运动,根据运动的合成和分解分别对水平方向和竖直方向列式,联立可求得电场强度和初速度;
(2)由位移公式可求得运动时间,再由动能定理可求得小球运动到距地面的高度为$\frac{h}{2}$时的动能
解答 解:(1)小球水平方向作匀减速直线运动,竖直方向做自由落体运动,设飞行时间为t,初速度为v0,则水平方向上有:
0-v0=-$\frac{Eqt}{m}$
0-v02=-$\frac{2EqL}{m}$
竖直方向上有:h=$\frac{1}{2}$gt2
整理可得:E=$\frac{mgL}{qh}$
v0=$\frac{L\sqrt{2gh}}{h}$
(2)设小球下落到$\frac{1}{2}$h时的动能为EK,此时小球的水平位移为S
S=v0t1-$\frac{1}{2}$$\frac{Eq}{m}$t12
t1=$\sqrt{\frac{h}{g}}$
由动能定理可得:$\frac{1}{2}$mgh-EqS=EK-$\frac{1}{2}$mv02
整理可得:EK=$\frac{1}{2}$mg[h+(3-2$\sqrt{2}$)$\frac{{L}^{2}}{h}$]
答:(1)电场强度E的大小为$\frac{mgL}{qh}$;水平初速度V0的大小为$\frac{L\sqrt{2gh}}{h}$;
(2)小球运动到距地面的高度为$\frac{h}{2}$时的动能为$\frac{1}{2}$mg[h+(3-2$\sqrt{2}$)$\frac{{L}^{2}}{h}$].
点评 此题关键根据小球的运动情景,建立运动模型,由于小球运动过程中,受到的电场力和重力是恒力,运用运动的分解的观点解决是常用的方法.

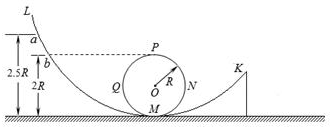
| A. | 若将小球从LM轨道上a点由静止释放,小球一定能沿轨道运动到K点 | |
| B. | 若将小球从LM轨道上b点由静止释放,小球一定能沿轨道运动到K点 | |
| C. | 若将小球从LM轨道上a、b点之间任一位置由静止释放,小球一定能沿轨道运动到K点 | |
| D. | 若将小球从LM轨道上a点以上任一位置由静止释放,小球沿轨道运动到K点后做斜上抛运动,小球做斜上抛运动时距离地面的最大高度一定小于由静止释放时的高度 |
| A. | 该粒子的动能一定增加 | |
| B. | 该粒子的动能可能始终不变 | |
| C. | 该粒子的电势能一定增加 | |
| D. | 只有是匀强电场才可以求出A、B两点间的电势差 |
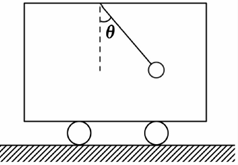 一辆小车在水平面上运动,悬挂的摆球相对小车静止并与竖直方向成θ角,如图所示,下列说法正确的是( )
一辆小车在水平面上运动,悬挂的摆球相对小车静止并与竖直方向成θ角,如图所示,下列说法正确的是( )| A. | 小车一定向左做匀加速直线运动 | |
| B. | 小车的加速度大小为gtanθ,方向向左 | |
| C. | 悬绳的拉力一定大于小球的重力 | |
| D. | 小球所受合外力方向一定向左 |
| A. | 原子核发生衰变时要遵守电荷守恒和质量守恒的规律 | |
| B. | 根据爱因斯坦的“光子说”可知光的波长越大,光子的能量越小 | |
| C. | 由波尔理论知道氢原子从激发态跃迁到基态时只能辐射特定频率的光子 | |
| D. | 发生光电效应时光电子的动能只与入射光的强度有关 | |
| E. | 天然放射现象与原子核内部变化有关 |
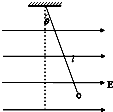 如图所示,一根长为l的细绝缘线,上端固定,下端系一个质量为m的带电小球,将整个装置放入一匀强电场,电场强度大小为E,方向水平向右,已知:当细线偏离竖直方向为θ=37°时,小球处于平衡状态,(sin37°=0.6 g取10)试求:
如图所示,一根长为l的细绝缘线,上端固定,下端系一个质量为m的带电小球,将整个装置放入一匀强电场,电场强度大小为E,方向水平向右,已知:当细线偏离竖直方向为θ=37°时,小球处于平衡状态,(sin37°=0.6 g取10)试求: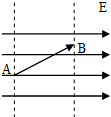 如图,匀强电场的场强E=100V/m,A,B两点相距0.1m,AB连线与电场线的夹角为60度,则AB两点的电势差为多少?
如图,匀强电场的场强E=100V/m,A,B两点相距0.1m,AB连线与电场线的夹角为60度,则AB两点的电势差为多少? 如图,长度为d的绝缘轻杆一端套在光滑水平转轴O上,另一端固定一质量为m电荷量为q的带负电小球,小球可以在竖直平面内做圆周运动,AC和BD分别为圆的竖直和水平直径,等量异种点电荷+Q、-Q分别固定在以C为中点、间距为2d的水平线上的E、F两点,让小球从最高点A由静止开始运动,经过B点时小球的速度大小为v,不考虑q对+Q,-Q所产生电场的影响.求小球:
如图,长度为d的绝缘轻杆一端套在光滑水平转轴O上,另一端固定一质量为m电荷量为q的带负电小球,小球可以在竖直平面内做圆周运动,AC和BD分别为圆的竖直和水平直径,等量异种点电荷+Q、-Q分别固定在以C为中点、间距为2d的水平线上的E、F两点,让小球从最高点A由静止开始运动,经过B点时小球的速度大小为v,不考虑q对+Q,-Q所产生电场的影响.求小球: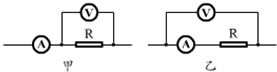 (1)用伏安法测某一电阻时,如果采用如图所示的甲电路,测量值为R1,如果采用乙电路,测量值为R2,那么R1、R2与真实值R之间满足关系C
(1)用伏安法测某一电阻时,如果采用如图所示的甲电路,测量值为R1,如果采用乙电路,测量值为R2,那么R1、R2与真实值R之间满足关系C