题目内容
2. 如图所示,质量为1kg的物体,以某一初速度v.从A点向下沿光滑的轨道运动,圆轨道半径为R=10m,不计空气阻力,若物体通过B点时的速度为30m/s,求:
如图所示,质量为1kg的物体,以某一初速度v.从A点向下沿光滑的轨道运动,圆轨道半径为R=10m,不计空气阻力,若物体通过B点时的速度为30m/s,求:(1)物体在A点时的速度.
(2)物体离开C点后还能上升多高?
分析 (1)对AB过程,由动能定理可求得物体在A点的速度;
(2)整个过程中物体的机械能守恒,根据机械能守恒可以求得能上升的最大高度.
解答 解:(1)对AB过程由动能定理可知:
mg(3R)=$\frac{1}{2}m{{v}_{B}}^{2}-\frac{1}{2}m{{v}_{A}}^{2}$
解得A点的速度为:vA=$10\sqrt{3}m/s$
(2)从B点开始分析,对B以后及到达最高点的过程,由机械能守恒定律可知:
$\frac{1}{2}m{{v}_{B}}^{2}$=mg(R+h)
解得:h=35m
答:(1)物体在A点时的速度为$10\sqrt{3}m/s$.
(2)物体离开C点后还能上升的高度为35m.
点评 本题是对动能定理的直接应用的考查,要注意正确做好受力分析,明确物理过程,再由动能定理列式求解即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6. 如图所示有三个质量相等,分别带有正电、负电和不带电的微粒,从极板左侧中央以相同的水平初速度v先后垂直场强射入,分别落到极板A、B、C处,如图所示,则下列说法正确的有( )
如图所示有三个质量相等,分别带有正电、负电和不带电的微粒,从极板左侧中央以相同的水平初速度v先后垂直场强射入,分别落到极板A、B、C处,如图所示,则下列说法正确的有( )
 如图所示有三个质量相等,分别带有正电、负电和不带电的微粒,从极板左侧中央以相同的水平初速度v先后垂直场强射入,分别落到极板A、B、C处,如图所示,则下列说法正确的有( )
如图所示有三个质量相等,分别带有正电、负电和不带电的微粒,从极板左侧中央以相同的水平初速度v先后垂直场强射入,分别落到极板A、B、C处,如图所示,则下列说法正确的有( )| A. | 粒子A带正电,B不带电,C带负电 | |
| B. | 三个粒子在电场中运动时间相等 | |
| C. | 三个粒子在电场中运动的加速度aA<aB<aC | |
| D. | 三个粒子到达极板时的动能EKA<EKB<EKC |
13.两个小球沿同一直线相向运动,动量大小均为2kg•m/s,碰后关于两小球的状态,不可能的是( )
| A. | 两球都静止 | |
| B. | 两球反向运动,动量大小均为2kg•m/s | |
| C. | 两球向同一方向运动 | |
| D. | 两球反向运动,动量大小均为1kg•m/s |
10. 如图所示,质量均为m的物体A、B通过一劲度系数为k的轻弹簧相连,开始时B放在地面上,A、B都处于静止状态.现用手通过细绳缓慢地将A向上提升距离L1时,B刚要离开地面,此过程手做功W1、手做功的平均功率为P1;若将A加速向上提起,A上升的距离为L2时,B刚要离开地面,此过程手做功W2、手做功的平均功率为P2,假设弹簧一直在弹性限度范围内,则( )
如图所示,质量均为m的物体A、B通过一劲度系数为k的轻弹簧相连,开始时B放在地面上,A、B都处于静止状态.现用手通过细绳缓慢地将A向上提升距离L1时,B刚要离开地面,此过程手做功W1、手做功的平均功率为P1;若将A加速向上提起,A上升的距离为L2时,B刚要离开地面,此过程手做功W2、手做功的平均功率为P2,假设弹簧一直在弹性限度范围内,则( )
 如图所示,质量均为m的物体A、B通过一劲度系数为k的轻弹簧相连,开始时B放在地面上,A、B都处于静止状态.现用手通过细绳缓慢地将A向上提升距离L1时,B刚要离开地面,此过程手做功W1、手做功的平均功率为P1;若将A加速向上提起,A上升的距离为L2时,B刚要离开地面,此过程手做功W2、手做功的平均功率为P2,假设弹簧一直在弹性限度范围内,则( )
如图所示,质量均为m的物体A、B通过一劲度系数为k的轻弹簧相连,开始时B放在地面上,A、B都处于静止状态.现用手通过细绳缓慢地将A向上提升距离L1时,B刚要离开地面,此过程手做功W1、手做功的平均功率为P1;若将A加速向上提起,A上升的距离为L2时,B刚要离开地面,此过程手做功W2、手做功的平均功率为P2,假设弹簧一直在弹性限度范围内,则( )| A. | W1=W2 | B. | P1<P2 | C. | L2=L1=$\frac{2mg}{k}$ | D. | L2>L1=$\frac{mg}{k}$ |
17. 如图所示小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面,不计一切阻力,下列说法正确的是( )
如图所示小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面,不计一切阻力,下列说法正确的是( )
 如图所示小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面,不计一切阻力,下列说法正确的是( )
如图所示小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面,不计一切阻力,下列说法正确的是( )| A. | 小球落地点离O点的水平距离为2R | |
| B. | 小球落地点时的动能为$\frac{5mgR}{2}$ | |
| C. | 小球运动到半圆弧最高点P时向心力恰好为零 | |
| D. | 小球在o点的支持力为2mg |
11.某学习小组为了探究做功与速度变化的关系,做了如下的实验:
A.按装置图(图1)安装好实验器材;
B.将木板固定,打点计时器的一端稍微垫高,在不连接橡皮筋的情况下,使小车能牵引纸带在木板上做匀速运动;
C.先用一条橡皮筋做实验,把橡皮筋拉伸到一定的长度,整理好纸带,接通电源,放开小车,打出一条纸带,用打点计时器打出的纸带测出小车的最大速度,记为v1,设此时橡皮筋对小车做功为W1,将数据记入表格;
D.改用2条、3条、4条„„橡皮筋重复上述实验,记录橡皮筋做功2W、3W、4W…情况下小车获得的速度v2、v3、v4…
E.分析数据,研究W与v的关系
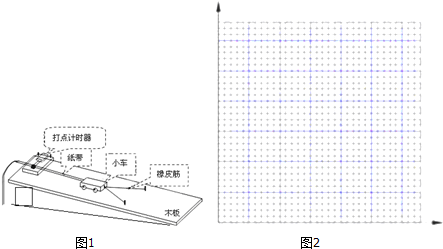
(1)为能完成这个探究的目的,请你把步骤C中划线部分补充完整:把橡皮筋拉伸到一定的长度,整理好纸带,接通电源,放开小车,打出一条纸带
(2)请你根据实验得出的数据在如图2所示的坐标系中作出相应的图象,得出的结论是橡皮筋对小车做功与小车速度的平方成正比
A.按装置图(图1)安装好实验器材;
B.将木板固定,打点计时器的一端稍微垫高,在不连接橡皮筋的情况下,使小车能牵引纸带在木板上做匀速运动;
C.先用一条橡皮筋做实验,把橡皮筋拉伸到一定的长度,整理好纸带,接通电源,放开小车,打出一条纸带,用打点计时器打出的纸带测出小车的最大速度,记为v1,设此时橡皮筋对小车做功为W1,将数据记入表格;
D.改用2条、3条、4条„„橡皮筋重复上述实验,记录橡皮筋做功2W、3W、4W…情况下小车获得的速度v2、v3、v4…
E.分析数据,研究W与v的关系

(1)为能完成这个探究的目的,请你把步骤C中划线部分补充完整:把橡皮筋拉伸到一定的长度,整理好纸带,接通电源,放开小车,打出一条纸带
(2)请你根据实验得出的数据在如图2所示的坐标系中作出相应的图象,得出的结论是橡皮筋对小车做功与小车速度的平方成正比
| 次数 | 小车速度v(m/s) | 小车速度的二次方v2(m/s)2 |
| 1 | 1.41 | 1.99 |
| 2 | 2.00 | 4.00 |
| 3 | 2.20 | 4.84 |
| 4 | 2.83 | 8.01 |
| 5 | 3.16 | 9.99 |
 如图为“碰撞中的动量守恒”实验装置示意图
如图为“碰撞中的动量守恒”实验装置示意图 某压榨机的结构示意图如图所示,其中B为固定铰链,若在A铰链处作用一垂直于墙壁的力F,则由于力F的作用,使滑块C压紧物体D,设C与D光滑接触,杆的重力及滑块C的重力不计,图中a=0.5m,b=0.05m,则物体D所受压力的大小与力F的比值为( )
某压榨机的结构示意图如图所示,其中B为固定铰链,若在A铰链处作用一垂直于墙壁的力F,则由于力F的作用,使滑块C压紧物体D,设C与D光滑接触,杆的重力及滑块C的重力不计,图中a=0.5m,b=0.05m,则物体D所受压力的大小与力F的比值为( )