题目内容
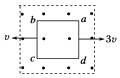
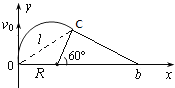
【题目】一质量为m,带电量为q的粒子,以速度v0从O点沿y轴正方向射入磁感强度为B的一圆形匀强磁场区域,磁场方向垂直于纸面,粒子飞出磁场区域后,从b处穿过x轴,速度方向与x轴正方向夹角为30°,如图,不计粒子重力,求: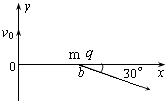
(1)圆形磁场区域的最小面积;
(2)粒子从O进入磁场区域到达b点所经历的时间及b点的坐标.
【答案】
(1)解:带电粒子在磁场中运动时,洛仑兹力提供向心力,则有
qv0B=m ![]()
解得,R= ![]()
带电粒子在磁场中做匀速圆周运动,连接粒子在磁场区入射点O和出射点c得弦长为 l=2Rsin60°= ![]()
如图所示,圆形磁场区域最小面积为OC为直径的圆,则磁场的半径为r= ![]() .
.
故圆形磁场区域的最小面积为 Smin=πr2
联立解得,Smin= ![]()
答:圆形磁场区域的最小面积是 ![]() ;
;
(2)解:带电粒子在磁场中轨迹圆弧对应的圆心角为120°,带电粒子在磁场中运动的时间为转动周期的 ![]() ,即t1=
,即t1= ![]() =
= ![]()
由几何知识得:cb=l= ![]()
粒子离开磁场从c到b点的运动时间为 t2= ![]() =
= ![]()
故粒子从O进入磁场区域到达b点所经历的时间t=t1+t2= ![]() +
+ ![]() .
.
b点的坐标x=ob=2lcos30°=3R= ![]() .
.
答:粒子从O进入磁场区域到达b点所经历的时间是 ![]() +
+ ![]() .b点的坐标是
.b点的坐标是 ![]() .
.
【解析】(1)根据带电粒子在磁场中运动时,洛仑兹力提供向心力即可求得半径;连接粒子在磁场区入射点和出射点的弦长ob,最小面积为ob为直径的圆.求出半径即可求得面积.(2)带电粒子在磁场中轨迹圆弧对应的圆心角为120°,根据圆心角与周期的关系即可求解运动时间;由几何知识求出b点的坐标.

 名校课堂系列答案
名校课堂系列答案【题目】小灯泡灯丝的电阻随温度的升高而变大,某同学利用实验探究这一现象.所提供的器材有:
A.电流表(A1)量程0﹣0.6A,内阻约0.125Ω
B.电流表(A2)量程0﹣3A,内阻约0.025Ω
C.电压表(V1)量程0﹣3V,内阻约3kΩ
D.电压表(V2)量程0﹣15V,内阻约15kΩ
E.滑动变阻器(R1)总阻值约10Ω
F.滑动变阻器(R2)总阻值约200Ω
G.电池(E)电动势3.0V,内阻很小
H.导线若干,电键K
该同学选择仪器,设计电路并进行实验,通过实验得到如下数据:
I/A | 0 | 0.12 | 0.21 | 0.29 | 0.34 | 0.38 | 0.42 | 0.45 | 0.47 | 0.49 | 0.50 |
U/V | 0 | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 | 1.20 | 1.40 | 1.60 | 1.80 | 2.00 |
(1)请你推测该同学选择的器材是:电流表为 , 电压表为 , 滑动变阻器为(以上均填写器材代号).
(2)请你推测该同学设计的实验电路图并画在图甲的方框中.
(3)请在图乙的坐标系中画出小灯泡的I﹣U曲线.
(4)若将该小灯泡直接接在电动势是 1.5V,内阻是 2.0Ω的电池两端,小灯泡的实际功率为W.
【题目】实验小组要测量一节干电池的电动势和内电阻.实验室有如下器材可供选择:
A.待测干电池(电动势约为1.5V,内阻约为1.0Ω)
B.电压表(量程3V)
C.电压表(量程15V)
D.电流表(量程0.6A)
E.定值电阻(阻值为50Ω)
F.滑动变阻器(阻值范围0~50Ω)
G.开关、导线若干
(1)为了尽量减小实验误差,在如图1所示的四个实验电路中应选用 . 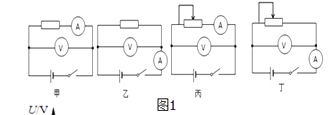
(2)实验中电压表应选用 . (选填器材前的字母)
(3)实验中测出几组电流表和电压表的读数并记录在下表中.
序号 | 1 | 2 | 3 | 4 | 5 | 6 |
电压U(V) | 1.45 | 1.40 | 1.30 | 1.25 | 1.20 | 1.10 |
电流I(A) | 0.060 | 0.120 | 0.240 | 0.260 | 0.360 | 0.480 |
请你将第5组数据描绘在图2中给出的U﹣I坐标系中并完成U﹣I 图线;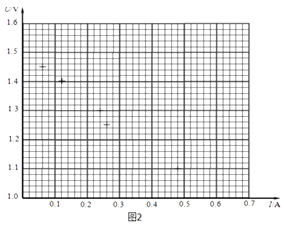
(4)由此可以得到,此干电池的电动势E=V,内电阻r=Ω.(结果均保留两位有效数字)
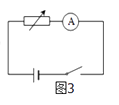
(5)有位同学从实验室找来了一个电阻箱,用如图3所示的电路测量电池的电动势和内电阻.闭合开关后,改变电阻箱阻值.当电阻箱阻值为R1时,电流表示数为I1;当电阻箱阻值为R2时,电流表示数为I2 . 已知电流表的内阻为RA . 请你用RA、R1、R2、I1、I2表示出电池的内电阻r= .