题目内容
在方向水平的匀强电场中,一不可伸长的不导电细线的一端连着一个质量为m的带电小球,另一端固定于O点,把小球拉起直至细线与场强平行,然后无初速释放.已知小球摆到最低点的另一侧,线与竖直方向的最大夹角为θ(如图),求小球经过最低点时细线对小球的拉力.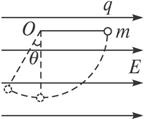
mg(3-
)
解析：设细线长为l,球的电荷量为q,场强为E.若电荷量q为正,则场强方向在题图中向右,反之向左,从释放点到左侧最高点,重力势能的减少等于电势能的增加,即mglcosθ=qEl(1+sinθ)
若小球运动到最低点时的速度为v,此时线的拉力为F,由功能关系得
mv2=mgl-qEl
由牛顿第二定律得F-mg=m
由以上各式解得F=mg(3-
).
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在方向水平的匀强电场中，一不可伸长的绝缘细线一端连着一个质量为m、电荷量为+q的带电小球，另一端固定于O点，将小球拉起直至细线与场强平行，然后无初速释放，则小球沿圆弧做往复运动．已知小球摆到最低点的另一侧时，线与竖直方向的最大夹角为θ（如图）．求：
在方向水平的匀强电场中，一不可伸长的绝缘细线的一端连着一个质量为m的带电小球，另一端固定于O点．把小球拉起直至细线与场强平行，然后无初速度释放．已知小球摆到最低点的另一侧，线与竖直方向的最大夹角为θ．则小球电性为
如图所示，在方向水平的匀强电场中，一不可伸长的不导电 细线长为L，一端连着一个质量为m，带电量为q小球，另一端固定于O点，把小球拉起直至细线与场强平行，然后无初速由A点释放，已知细线转过60°角，小球到达B点时速度恰为零．求：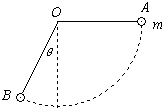
在方向水平的匀强电场中，绝缘细线的一端连着一个质量为m的带电小球，另一端悬挂于O点．将小球拿到A点（此时细线与电场方向平行）无初速释放，已知小球摆到B点时速度为零，此时细线与竖直方向的夹角为θ=30°，求：
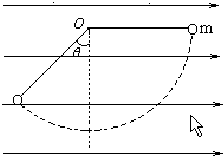在方向水平的匀强电场中，一根长为L=0.4米，不可伸长的不导电细线，其一端连着一个质量为m=1kg的带正电小球，另一端固定于O点．把小球拉起直至细线与场强平行，然后无初速释放．已知小球摆到最低点的另一侧，线与竖直方向的最大夹角为θ=30°（如图）．g取10m/s2．求：