题目内容
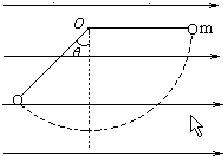 在方向水平的匀强电场中,一根长为L=0.4米,不可伸长的不导电细线,其一端连着一个质量为m=1kg的带正电小球,另一端固定于O点.把小球拉起直至细线与场强平行,然后无初速释放.已知小球摆到最低点的另一侧,线与竖直方向的最大夹角为θ=30°(如图).g取10m/s2.求:
在方向水平的匀强电场中,一根长为L=0.4米,不可伸长的不导电细线,其一端连着一个质量为m=1kg的带正电小球,另一端固定于O点.把小球拉起直至细线与场强平行,然后无初速释放.已知小球摆到最低点的另一侧,线与竖直方向的最大夹角为θ=30°(如图).g取10m/s2.求:(1)小球经过最低点时细线对小球的拉力;
(2)小球在下摆过程中获得的最大动能.
分析:(1)由动能定理求出小球受到的电场力,由动能定理研究小球从释放到最低点的过程求出小球到最低点的速度,
经过最低点时,由重力和细线的拉力的合力提供小球的向心力,由牛顿第二定律求出细线对小球的拉力.
(2)确定出速度最大的位置,由动能定理求出小球的最大动能.
经过最低点时,由重力和细线的拉力的合力提供小球的向心力,由牛顿第二定律求出细线对小球的拉力.
(2)确定出速度最大的位置,由动能定理求出小球的最大动能.
解答:解:(1)小球无初速度释放摆到另一侧的过程:
由动能定理得:mgLcosθ-qEL(1+sinθ)=0-0,
解得:qE=
mg;
小球摆到最低点过程中,由动能定理得:mgL-qEL=
mv2-0,
小球最低点时由重力和细线的拉力的合力提供小球的向心力,
由牛顿第二定律得:F-mg=m
,
解得:F=
N≈18.45N;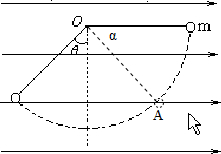
(2)将电场力与重力合成F合=
mg,
由图可知,合力方向与竖直方向成30度角斜向右下,A为对应的“等效最低点”.
由几何关系得 α=60°,小球到达A时速度最大,动能最大,
小球从释放到小球到达A点过程中,由动能定理得:
mgLsinα-qEL(1-cosα)=
mv′2-0,
解得小球的最大动能:EK=
mv′2≈1.33J;
答:(1)小球经过最低点时细线对小球的拉力为18.45N;
(2)小球在下摆过程中获得的最大动能为1.33J.
由动能定理得:mgLcosθ-qEL(1+sinθ)=0-0,
解得:qE=
| ||
| 3 |
小球摆到最低点过程中,由动能定理得:mgL-qEL=
| 1 |
| 2 |
小球最低点时由重力和细线的拉力的合力提供小球的向心力,
由牛顿第二定律得:F-mg=m
| v2 |
| L |
解得:F=
10(9-2
| ||
| 3 |

(2)将电场力与重力合成F合=
2
| ||
| 3 |
由图可知,合力方向与竖直方向成30度角斜向右下,A为对应的“等效最低点”.
由几何关系得 α=60°,小球到达A时速度最大,动能最大,
小球从释放到小球到达A点过程中,由动能定理得:
mgLsinα-qEL(1-cosα)=
| 1 |
| 2 |
解得小球的最大动能:EK=
| 1 |
| 2 |
答:(1)小球经过最低点时细线对小球的拉力为18.45N;
(2)小球在下摆过程中获得的最大动能为1.33J.
点评:本题是带电物体在电场中圆周运动问题,动能定理和向心力结合是常用的解题方法.常见的题型.对于多过程的问题可能多次应用动能定理求解问题.
第2问是就是等效重力场的问题,找出对应的“等效最低点”去解决问题.
第2问是就是等效重力场的问题,找出对应的“等效最低点”去解决问题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
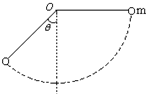 在方向水平的匀强电场中,一不可伸长的绝缘细线一端连着一个质量为m、电荷量为+q的带电小球,另一端固定于O点,将小球拉起直至细线与场强平行,然后无初速释放,则小球沿圆弧做往复运动.已知小球摆到最低点的另一侧时,线与竖直方向的最大夹角为θ(如图).求:
在方向水平的匀强电场中,一不可伸长的绝缘细线一端连着一个质量为m、电荷量为+q的带电小球,另一端固定于O点,将小球拉起直至细线与场强平行,然后无初速释放,则小球沿圆弧做往复运动.已知小球摆到最低点的另一侧时,线与竖直方向的最大夹角为θ(如图).求: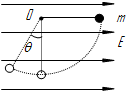 在方向水平的匀强电场中,一不可伸长的绝缘细线的一端连着一个质量为m的带电小球,另一端固定于O点.把小球拉起直至细线与场强平行,然后无初速度释放.已知小球摆到最低点的另一侧,线与竖直方向的最大夹角为θ.则小球电性为
在方向水平的匀强电场中,一不可伸长的绝缘细线的一端连着一个质量为m的带电小球,另一端固定于O点.把小球拉起直至细线与场强平行,然后无初速度释放.已知小球摆到最低点的另一侧,线与竖直方向的最大夹角为θ.则小球电性为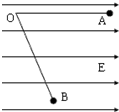 如图所示,在方向水平的匀强电场中,一不可伸长的不导电 细线长为L,一端连着一个质量为m,带电量为q小球,另一端固定于O点,把小球拉起直至细线与场强平行,然后无初速由A点释放,已知细线转过60°角,小球到达B点时速度恰为零.求:
如图所示,在方向水平的匀强电场中,一不可伸长的不导电 细线长为L,一端连着一个质量为m,带电量为q小球,另一端固定于O点,把小球拉起直至细线与场强平行,然后无初速由A点释放,已知细线转过60°角,小球到达B点时速度恰为零.求: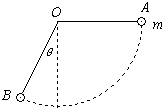 在方向水平的匀强电场中,绝缘细线的一端连着一个质量为m的带电小球,另一端悬挂于O点.将小球拿到A点(此时细线与电场方向平行)无初速释放,已知小球摆到B点时速度为零,此时细线与竖直方向的夹角为θ=30°,求:
在方向水平的匀强电场中,绝缘细线的一端连着一个质量为m的带电小球,另一端悬挂于O点.将小球拿到A点(此时细线与电场方向平行)无初速释放,已知小球摆到B点时速度为零,此时细线与竖直方向的夹角为θ=30°,求: