题目内容
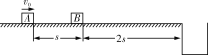
【题目】在水平地面上沿直线放置两个完全相同的小物体A和B，它们相距s，在距B为2s的右侧有一坑，如图所示，A以初速度v0向B运动，为使A能与B发生碰撞且碰后又不会落入坑中，求A、B与水平地面间的动摩擦力因数满足的条件，已知A、B碰撞时间很短且碰后粘在一起不再分开，重力加速度为g．
【答案】
>μ≥
【解析】
试题分析：设A、B质量均为m，它们与地面间的动摩擦因数为μ，
若A能与B相碰，则有：
mv－μmgs>0 ①
设A与B碰前速度为v1，碰后速度为v2，由动能定理得：
mv－mv＝μmgs ②
碰撞过程中，动量守恒，以A的速度方向为正，
根据动量守恒定律得：mv1＝2mv2 ③
A、B粘一起不落入坑中的条件为：×2mv≤μ·2mg·2s ④
联立并解得：>μ≥
练习册系列答案
相关题目
