题目内容
如图所示,在斜面倾角为θ的斜面底端,垂直斜面有一固定挡板。现有一质量为m(可视为质点)的物块以速度v0从P点沿斜面下滑,已知物块与斜面间动摩擦因数为μ(μ<tanθ),P点距离挡板距离为L,物块与挡板碰撞时无能量损失,不计空气阻力,则有关下列说法正确的是:
A.物块第一次与挡板碰撞时的动能为 |
| B.第一次与挡板碰后沿斜面上滑的最大距离一定小于L |
C.从开始到物块静止,物块重力势能的减少量为 |
D.物块在斜面上通过的总路程为 |
CD
解析试题分析:根据动能定理,在下落到挡板前设碰撞前速度为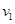 ,利用动能定理则
,利用动能定理则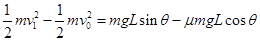 ,所以A错。假设物体初速度为0,则第一次与挡板碰后沿斜面上滑的最大距离一定小于L,但由于有初速度,初速度对应的动能可能大于摩擦力消耗的能量,因此B错。从开始到物块静止,物块重力势能的减少量为
,所以A错。假设物体初速度为0,则第一次与挡板碰后沿斜面上滑的最大距离一定小于L,但由于有初速度,初速度对应的动能可能大于摩擦力消耗的能量,因此B错。从开始到物块静止,物块重力势能的减少量为 ,正确。利用动能定理,则块在斜面上通过的总路程为s,即
,正确。利用动能定理,则块在斜面上通过的总路程为s,即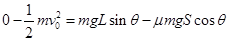 ,化简则
,化简则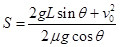
考点:动能定理
点评:本题考查了通过动能定理分析物体在外力作用下动能变化。

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 如图所示,在斜面倾角为θ的斜面底端,垂直斜面有一固定挡板.现有一质量为m(可视为质点)的物块以速度v0从P点沿斜面下滑,已知物块与斜面间动摩擦因数为μ(μ<tanθ),P点距离挡板距离为L,物块与挡板碰撞时无能量损失,不计空气阻力,则有关下列说法正确的是( )
如图所示,在斜面倾角为θ的斜面底端,垂直斜面有一固定挡板.现有一质量为m(可视为质点)的物块以速度v0从P点沿斜面下滑,已知物块与斜面间动摩擦因数为μ(μ<tanθ),P点距离挡板距离为L,物块与挡板碰撞时无能量损失,不计空气阻力,则有关下列说法正确的是( )A、物块第一次与挡板碰撞时的动能为mgLsinθ+
| ||||
| B、第一次与挡板碰后沿斜面上滑的最大距离一定小于L | ||||
| C、从开始到物块静止,物块重力势能的减少量为mgLsinθ | ||||
D、物块在斜面上通过的总路程为
|
 在倾角为θ=30°的足够长的斜面底端,木块A以某一初速度v0沿斜面向上运动,若木块与斜面间的动摩擦因数μ=
在倾角为θ=30°的足够长的斜面底端,木块A以某一初速度v0沿斜面向上运动,若木块与斜面间的动摩擦因数μ=



