题目内容
15. 如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量均为Q,其中A带正电荷,B带负电荷,D、C是它们连线的垂直平分线,A、B、C三点构成一边长为d的等边三角形,另有一个带电小球E,质量为m、电荷量为+q(可视为点电荷),被长为L的绝缘轻质细线悬挂于O点,O点在C点的正上方.现在把小球E拉到M点,使细线水平绷紧且与A、B、C处于同一竖直面内,并由静止开始释放,小球E向下运动到最低点C时,速度为v.已知静电力常量为k,重力加速度为g,试求:
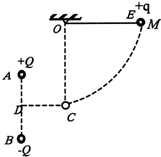
如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量均为Q,其中A带正电荷,B带负电荷,D、C是它们连线的垂直平分线,A、B、C三点构成一边长为d的等边三角形,另有一个带电小球E,质量为m、电荷量为+q(可视为点电荷),被长为L的绝缘轻质细线悬挂于O点,O点在C点的正上方.现在把小球E拉到M点,使细线水平绷紧且与A、B、C处于同一竖直面内,并由静止开始释放,小球E向下运动到最低点C时,速度为v.已知静电力常量为k,重力加速度为g,试求:(1)带电小球E在C点所受的库仑力的大小及方向;
(2)绝缘细线在C点对带电小球E的拉力T;
(3)取D点的电势为零,求A、B所形成的电场中,M点的电势φM.
分析 (1)根据库仑定律和电场力的合成,求小球E在C点所受的库仑力的大小及方向.
(2)小球做圆周运动,在C点,由牛顿第二定律可求得细绳对小球E的拉力T.
(2)由W=Uq即可求得MC两点间的电势差,则可求得M点的电势.
解答 解:(1)在C点时正电荷A对小球E的场力F1与负电荷B对小球E的电场力F2相等,且为:
F1=F2=k$\frac{Qq}{{d}^{2}}$
又A、B、C为一等边三角形,所以F1、F2的夹角为120°,故F1、F2的合力为:
F=2F1cos60°=k$\frac{Qq}{{d}^{2}}$,方向竖直向下
(2)带电小球E在C点时,由牛顿第二定律得:
T-mg-F=m$\frac{{v}^{2}}{L}$
解得:T=mg+k$\frac{Qq}{{d}^{2}}$+m$\frac{{v}^{2}}{L}$
(2)电荷E从M点运动到C的过程中,电场力做正功,重力做正功.根据动能定理得:
qUMC+mgL=$\frac{1}{2}$mv2
得M、C两点的电势差为:UMC=$\frac{m{v}^{2}-2mgL}{2q}$
又C点与D点为等势点,UMC=φM-φC=,解得 M点的电势为:
φM=UMC=$\frac{m{v}^{2}-2mgL}{2q}$
答:(1)带电小球E在C点所受的库仑力的大小为k$\frac{Qq}{{d}^{2}}$,方向竖直向下;
(2)绝缘细线在C点对带电小球E的拉力T是mg+k$\frac{Qq}{{d}^{2}}$+m$\frac{{v}^{2}}{L}$;
(3)取D点的电势为零,A、B所形成的电场中,M点的电势φM是$\frac{m{v}^{2}-2mgL}{2q}$.
点评 本题考查电场中力与能的性质,要注意小球在拉力、重力及库仑力的作用下做圆周运动,应明确合力充当了向心力.

 阅读快车系列答案
阅读快车系列答案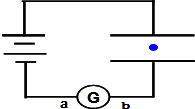 如图,将平行板电容器与电池两端相连,两极板间的带电尘埃恰好处于静止状态.若将上板缓慢地下移一些,其它条件不变,则( )
如图,将平行板电容器与电池两端相连,两极板间的带电尘埃恰好处于静止状态.若将上板缓慢地下移一些,其它条件不变,则( )| A. | 电容器内的电场强度不变,尘埃仍静止 | |
| B. | 电场强度变大,尘埃将向上做加速运动 | |
| C. | 电容器所带的电量减小 | |
| D. | 电容器所带的电量增加 |
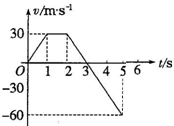 某军事试验场正在平地上试射地对空导弹,若某次竖直向上发射导弹时发生故障,导弹v-t图象如图所示,则下述说法中正确的是( )
某军事试验场正在平地上试射地对空导弹,若某次竖直向上发射导弹时发生故障,导弹v-t图象如图所示,则下述说法中正确的是( )| A. | 0~1 s内导弹匀速上升 | B. | 1 s~2 s内导弹静止不动 | ||
| C. | 3 s末导弹上升到最高点 | D. | 3 s~5s,导弹在下落过程 |
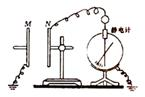 如图所示,由M、N两块相互靠近的平行金属板组成的平行板电容器,极板N与静电计的金属球相接,极板M与静电计的外壳均接地.给电容器充电,静电计指针张开一定角度.以下实验过程中电容器所带电荷量可认为不变,下面操作能使静电计指针张角变大的是( )
如图所示,由M、N两块相互靠近的平行金属板组成的平行板电容器,极板N与静电计的金属球相接,极板M与静电计的外壳均接地.给电容器充电,静电计指针张开一定角度.以下实验过程中电容器所带电荷量可认为不变,下面操作能使静电计指针张角变大的是( )| A. | 在M、N之间插入有机玻璃板 | |
| B. | 将M板沿水平向右方向靠近N板 | |
| C. | 将M板向上平移 | |
| D. | 在M、N之间插入金属板,且不和M、N接触 |
| A. | 光的波粒二象性学说是由牛顿的微粒说与惠更斯的波动的规律来描述 | |
| B. | 光的波粒二象性彻底推翻了麦克斯韦的电磁理论 | |
| C. | 光子说并没有否定光的电磁说,光子的能量E=hv,v表示光的频率,E表示粒子的能量 | |
| D. | 个别光子的行为表现为粒子性,大量光子的行为表现为波动性 |
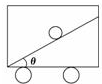 火车正沿水平直线做匀加速运动,在车厢中有一个装置所示,小球与光滑斜面相对静止,斜面与水平面的夹角为θ,根据这一现象判断火车的加速度方向及大小.
火车正沿水平直线做匀加速运动,在车厢中有一个装置所示,小球与光滑斜面相对静止,斜面与水平面的夹角为θ,根据这一现象判断火车的加速度方向及大小.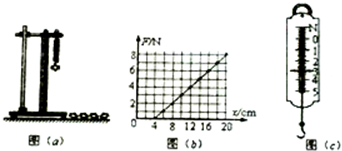 某同学在“验证力的平行四边形定则”的实验时,先探究了弹簧弹力大小与长度关系,实验装置如图a所示.弹簧处于竖直方向.他通过实验得到如图(b)所示的弹力大小F与弹簧长度x的关系图线.
某同学在“验证力的平行四边形定则”的实验时,先探究了弹簧弹力大小与长度关系,实验装置如图a所示.弹簧处于竖直方向.他通过实验得到如图(b)所示的弹力大小F与弹簧长度x的关系图线.